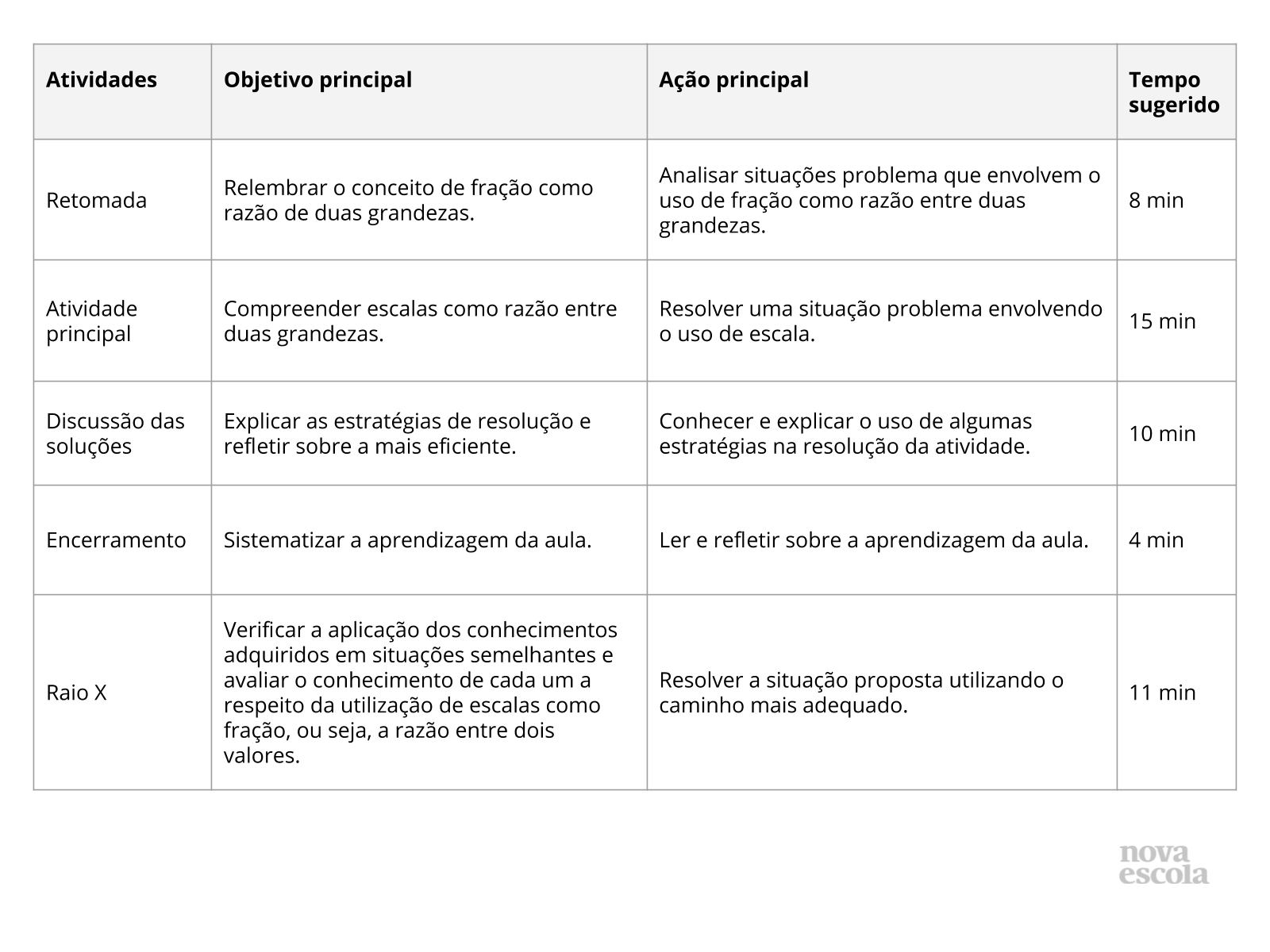
Atividade principal
Plano de Aula
Plano de aula: Comparando duas grandezas
Plano 2 de uma sequência de 5 planos. Veja todos os planos sobre As frações em nosso dia a dia
Por: Luiz Filipe Trovão
Descrição
Este plano de aula foi elaborado pelo Time de Autores NOVA ESCOLA
Autor: Luiz Filipe Trovão
Mentor: Ferdinando Caíque Genghini Dantas Lobo
Especialista: Luciana Maria Tenuta de Freitas
Habilidade da BNCC
EF07MA06 - Reconhecer que as resoluções de um grupo de problemas que têm a mesma estrutura podem ser obtidas utilizando os mesmo procedimentos.
EF07MA08 - Comparar e ordenar frações associadas às ideias de partes de inteiros, resultado da divisão, razão e operador.
EF07MA09 - Utilizar, na resolução de problemas, a associação entre razão e fração, como a fração 2/3 para expressar a razão de duas partes de uma grandeza para três partes da mesma ou três partes de outra grandeza.
Objetivos específicos
- Compreender frações como razão entre duas grandezas;
- Associar o conceito de escala a ideia de fração.
Conceito-chave
Escala como razão entre duas grandezas.
Recursos necessários
Lápis, borracha e caderno.
Habilidades BNCC:
Objetivos de aprendizagem
- Compreender frações como razão entre duas grandezas;
- Associar o conceito de escala a ideia de fração.
Resumo da aula
Orientações: Este slide não é um substituto para as anotações para o professor e não deve ser apresentado para os alunos. Trata-se apenas de um resumo da proposta para apoiá-lo na aplicação do plano em sala de aula.
Orientação: Leia atentamente o plano inteiro e as anotações para o professor. Busque antecipar quais questões podem surgir com a sua turma e preveja adequações ao nível em que seus alunos estão.
Compartilhe o objetivo da aula com os alunos antes de aplicar proposta.
Na aba “Sobre o plano”, confira os conhecimentos que sua turma já deve dominar para seguir essa proposta.
Se quiser salvar o plano no seu computador, faça download dos slides na aba “Materiais complementares”. Você também pode imprimi-lo clicando no botão “imprimir”.
Leituras:
- Nova ordem numérica: https://novaescola.org.br/conteudo/2657/nova-ordem-numerica
- Introdução aos números racionais: https://novaescola.org.br/conteudo/2722/introducao-aos-numeros-racionais
- Os elementos que compõem um mapa: https://novaescola.org.br/conteudo/206/os-elementos-que-compoem-um-mapa
- Sua turma sabe a função da escala?: https://novaescola.org.br/conteudo/2300/sua-turma-sabe-qual-a-funcao-da-escala
Objetivo

Tempo sugerido: 2 minutos.
Orientação: Projete ou leia o objetivo para a turma. Caso não seja possível a projeção, escreva o objetivo no quadro.
Propósito: Compartilhar o objetivo da aula.
Retomada

Tempo sugerido: 8 minutos (Slides 3 e 4)
Orientação: Professor, projete os slides para a sala. Caso não seja possível a projeção, leia o texto presente no balão do slide 3 e escreva no quadro os dois problemas presentes nos balões do slide 4.
Realize uma reflexão sobre o texto presente no balão de fala do slide 3, apontando que, como eles já viram anteriormente, as frações também são utilizadas como forma de comparar duas grandezas (ou quaisquer outros tipos de valores). Se necessário, explique para os aluno que grandeza é tudo o que se pode mensurar (medir): distância, massa, altura, valor monetário, entre outros.
No slide 4, explique que o nome dado a essa comparação por meio de uma fração é razão, realize as perguntas presentes nos dois balões de fala (uma da cada vez) e disponibilize tempo para que os alunos pensem sobre os questionamentos:
“Karla possui 20 lápis de cor em seu estojo, enquanto Roberta possui 10. Qual a relação entre a quantidade de lápis de cor de Roberta e a quantidade de lápis de cor de Karla?”
Resposta: 10/20 = 1/2 ? Isso significa que a cada 1 lápis que Roberta possui, Karla possui 2, ou Roberta possui metade da quantidade de lápis que Karla possui.
“Dênis possui R$ 200,00 em sua conta bancária, enquanto Rodolfo possui R$ R$ 300,00. Qual a relação entre a o valor que Dênis possui e o valor que Rodolfo possui?”
Resposta: 200/300 = 2/3 ? Isso significa que a cada R$ 2,00 que Dênis possui, Rodolfo possui R$ 3,00.
Finalize a retomada realizando a leitura do texto presente no final do slide.
Propósito: Relembrar o conceito de razão por meio de situações cotidianas de comparação de grandezas.
Discuta com a turma:
- Há alguma diferença entre comparar a quantidades de lápis entre a Karla/Roberta e Roberta/Karla?
- Há alguma diferença entre comparar os valores entre Dênis/Rodolfo e Rodolfo/Dênis?
- Uma fração sempre será uma razão?
- Uma razão sempre será uma fração?
Retomada

Tempo sugerido: 8 minutos (Slides 3 e 4)
Orientação: Professor, projete os slides para a sala. Caso não seja possível a projeção, leia o texto presente no balão do slide 3 e escreva no quadro os dois problemas presentes nos balões do slide 4.
Realize uma reflexão sobre o texto presente no balão de fala do slide 3, apontando que como eles já viram anteriormente, as frações também são utilizadas como forma de comparar duas grandezas (ou quaisquer outros tipos de valores). Se necessário, explique para os aluno que grandeza é tudo o que se pode mensurar (medir): distância, massa, altura, valor monetário entre outros.
No slide 4 explique que o nome dado a essa comparação por meio de uma fração é razão, realize as perguntas presentes nos dois balões de fala (uma da cada vez) e disponibilize tempo para que os alunos pensem sobre os questionamentos:
“Karla possui 20 lápis de cor em seu estojo, enquanto Roberta possui 10. Qual a relação entre a quantidade de lápis de cor de Roberta e a quantidade de lápis de cor de Karla?”
Resposta: 10/20 = 1/2 ? Isso significa que a cada 1 lápis que Roberta possui, Karla possui 2, ou Roberta possui metade da quantidade de lápis que Karla possui.
“Dênis possui R$ 200,00 em sua conta bancária, enquanto Rodolfo possui R$ R$ 300,00. Qual a relação entre a o valor que Dênis possui e o valor que Rodolfo possui?”
Resposta: 200/300 = 2/3 ? Isso significa que a cada R$ 2,00 que Dênis possui, Rodolfo possui R$ 3,00.
Finalize a retomada realizando a leitura do texto presente no final do slide.
Propósito: Relembrar o conceito de razão por meio de situações cotidianas de comparação de grandezas.
Discuta com a turma:
- Há alguma diferença entre comparar a quantidades de lápis entre a Karla/Roberta e Roberta/Karla?
- Há alguma diferença entre comparar os valores entre Dênis/Rodolfo e Rodolfo/Dênis?
- Uma fração sempre será uma razão?
- Uma razão sempre será uma fração?
Atividade principal

Tempo sugerido: 15 minutos.
Orientação: Imprima a atividade principal, entregue para os alunos e leia juntamente com eles a situação apresentada no exercício. Caso não seja possível a projeção, o professor poderá escrever a situação no quadro ou confeccionar um cartaz.
Explique para os alunos que a escala nesse exercício servirá para reduzir proporcionalmente o tamanho da cidade para a reprodução do mapa.
Peça para que eles se lembrem que para operacionalizar uma escala é necessário representá-la por uma fração, e a operação de multiplicação de uma fração por um número natural será muito importante na resolução desse exercício.
Dê exemplos como: ”A escala 1:20 é representada pela fração 1/20 (um vinte avos)”; “A escala 1:100 é representada pela fração 1/100 (um centésimo)”.
Após essas ações, disponibilize tempo para que eles resolvam os itens “a” e “b”.
Utilize o guia de intervenções para discutir com os alunos as possibilidades existentes na organização desse problema.
Propósito: Comparar duas grandezas de comprimento por meio da utilização da escala.
Discuta com a turma:
- O que a escala 1:3000 significa?
- É possível fazer esse mapa em uma única folha de caderno? Por quê?
Materiais complementares:
Discussão da solução

Tempo sugerido: 8 minutos (Slides 6 e 7).
Orientação: Inicialmente, peça para que os alunos discutam as soluções com o colega ao lado, sempre acompanhando-os em seus raciocínios.
Em seguida, peça para que alguns alunos exponham a resolução da atividade. A ideia não é direcionar para que determinado aluno apresente a solução, porém quanto mais caminhos diferentes forem apresentados para se chegar na mesma resposta, mais rica será a discussão.
Após os alunos compartilharem as estratégias utilizadas na resolução dos exercícios, passe para essa série de slides. Caso não seja possível a projeção dos slides, o professor deverá reproduzir, pelo menos, os valores do exercício e os cálculos realizados, no quadro ou em um cartaz, o restante da solução pode ser lida para a sala.
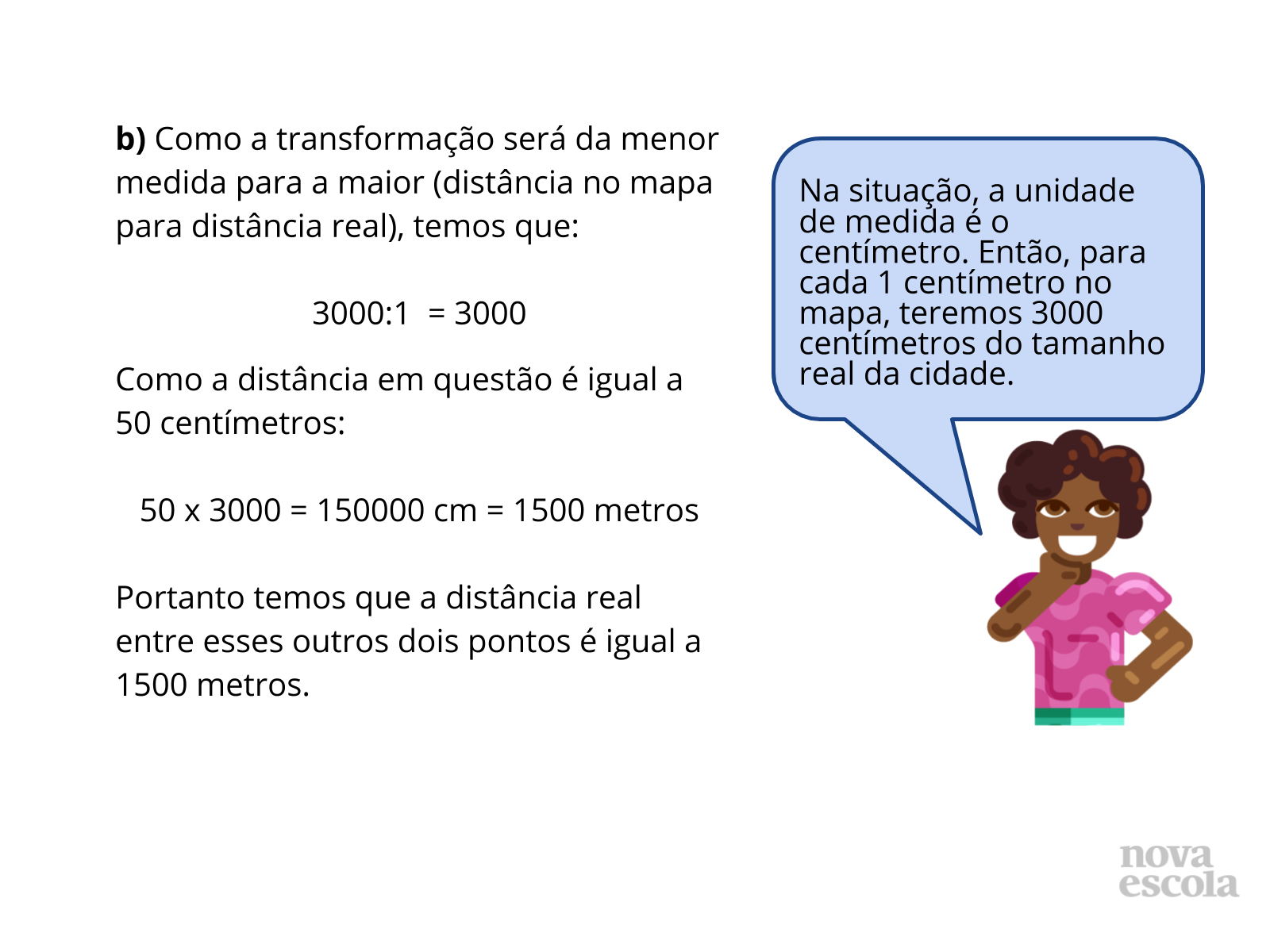
Na resolução do exercício, temos, no item “a”, a transformação da notação de escala para a notação de fração (visto que a transformação ocorrerá do maior valor para o menor), que será a utilizada para a realização dos cálculos.
Dando prosseguimento na resolução, temos o produto entre a distância real dos dois pontos da cidade pela fração, seguido de todas as simplificações e por último o quociente de 3/2, chegando assim ao valor que representa a distância proporcional na escala indicada, desses dois pontos da cidade, para a confecção do mapa.
Professor, aponte como outra maneira de resolver o item “a”, de forma mais rápida a divisão da distância entre os dois pontos, pela segunda parte da escala, nesse caso o 3000.
O item “b”, possui o caminho inverso do “a”, pois a transformação ocorrerá de uma distância do mapa para uma distância real, nesse caso a escala não será representada por uma fração e sim pelo maior no número, no caso o 3000. O restante do cálculo é similar ao item “a”, ou seja, é realizado o produto entre a escala e a distância, um detalhe a ser observado nesse item é que os alunos podem chegar na resposta em centímetros, estimule-os a dar mais um passo e chegar no valor, em metros.
Propósito: Apresentar e compartilhar meios utilizados na obtenção da solução, a fim de expor diferentes caminhos para se obter o mesmo resultado.
Discuta com a turma:
- É possível o valor da distância entre as duas cidades nesse mapa ser maior que o valor real?
- O que acontece com o valor da distância entre os dois pontos, após ser usada essa escala?
- Qual a diferença entre transformar uma medida real para uma medida no mapa e transformar uma medida do mapa em uma medida real?
Discussão da solução
Tempo sugerido: 8 minutos (Slides 6 e 7).
Orientação: Inicialmente, peça para que os alunos discutam as soluções com o colega ao lado, sempre acompanhando-os em seus raciocínios.
Em seguida, peça para que alguns alunos exponham a resolução da atividade. A ideia não é direcionar para que determinado aluno apresente a solução, porém quanto mais caminhos diferentes forem apresentados para se chegar na mesma resposta, mais rica será a discussão.
Após os alunos compartilharem as estratégias utilizadas na resolução dos exercícios, passe para essa série de slides. Caso não seja possível a projeção dos slides, o professor deverá reproduzir, pelo menos, os valores do exercício e os cálculos realizados, no quadro ou em um cartaz, o restante da solução pode ser lida para a sala.
Na resolução do exercício, temos, no item “a”, a transformação da notação de escala para a notação de fração (visto que a transformação ocorrerá do maior valor para o menor), que será a utilizada para a realização dos cálculos.
Dando prosseguimento na resolução, temos o produto entre a distância real dos dois pontos da cidade pela fração, seguido de todas as simplificações e por último o quociente de 3/2, chegando assim ao valor que representa a distância proporcional na escala indicada, desses dois pontos da cidade, para a confecção do mapa.
Professor, aponte como outra maneira de resolver o item “a”, de forma mais rápida a divisão da distância entre os dois pontos, pela segunda parte da escala, nesse caso o 3000.
O item “b”, possui o caminho inverso do “a”, pois a transformação ocorrerá de uma distância do mapa para uma distância real, nesse caso a escala não será representada por uma fração e sim pelo maior no número, no caso o 3000. O restante do cálculo é similar ao item “a”, ou seja, é realizado o produto entre a escala e a distância, um detalhe a ser observado nesse item é que os alunos podem chegar na resposta em centímetros, estimule-os a dar mais um passo e chegar no valor, em metros.
Propósito: Apresentar e compartilhar meios utilizados na obtenção da solução, a fim de expor diferentes caminhos para se obter o mesmo resultado.
Discuta com a turma:
- É possível o valor da distância entre as duas cidades nesse mapa ser maior que o valor real?
- O que acontece com o valor da distância entre os dois pontos, após ser usada essa escala?
- Qual a diferença entre transformar uma medida real para uma medida no mapa e transformar uma medida do mapa em uma medida real?
Encerramento

Tempo sugerido: 4 minutos
Orientação: Encerre a aula retomando a ideia de escala e apontando algumas de suas utilizações, conforme as informações do slide.
Retome a demonstração da escala que está no quadro, presente no slide. Finalize apontando outra forma mais simples, que já foi mencionada anteriormente na discussão da solução, que substitui o uso da fração pela simples divisão quando a intenção é reduzir algo, e no caso da ampliação a operação utilizada é a multiplicação.
Propósito: Realiza uma reflexão sobre os conteúdos aprendidos na aula.
Raio X
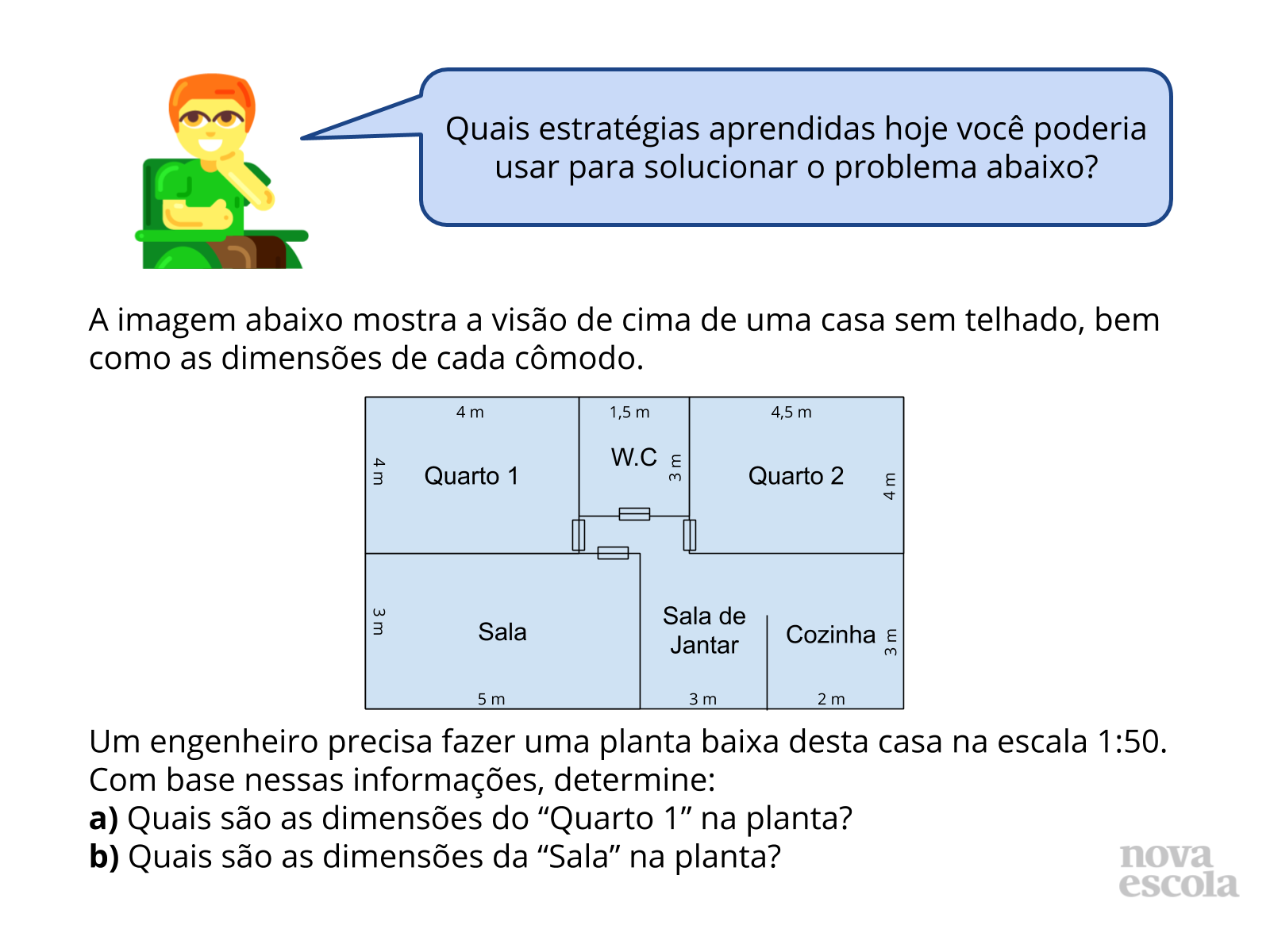
Tempo sugerido: 11 minutos.
Orientação: Apresente a nova situação e peça para que os alunos analisem e resolvam, em um primeiro momento individualmente e em seguida compartilhando a forma de pensar com o colega ao lado. Você pode projetar, passar no quadro ou fazer o download desta atividade e entregar para os seus alunos. O raio x é um momento para você avaliar se todos os estudantes conseguiram avançar no conteúdo proposto, então procure anotar e identificar todos os comentários que surgirem.
Propósito: Realizar uma atividade teórica relativa aos conteúdos ensinados na aula.
Discuta com a turma:
- O que significa a escala 1:50?
- Cada metro das dimensões reais da casa equivalem a quantos metros na planta?
Materiais complementares:
Para os alunos
Para o professor
Sugestão de adaptação para ensino remoto
Código do plano
MAT7_06NUM02
Recursos
- Necessários:
- caderno
- lápis
- régua
- grupo de alunos no WhatsApp
- Opcionais:
- Google Sala de Aula
Para este plano, foque na etapa: Atividade Principal
Aquecimento
A atividade é uma retomada de conceitos e relembrar o conceito de razão por meio de situações cotidianas de comparação de grandezas. Você pode propor os questionamentos apresentados no slide usando um editor de texto (Google Docs, por exemplo) que, de maneira colaborativa e síncrona, os alunos possam respondê-los, ou ainda usar a função de áudio do WhatsApp para que, um a um, postem suas respostas ou hipóteses sobre o assunto disparador. Oriente-os que é um momento de retomada de conteúdos e que caso tenham dúvidas, estas serão trabalhadas no decorrer da aula.
Atividade principal
Para a realização da atividade principal os alunos precisam ter acesso ao problema proposto. Para isso, fotografe a atividade principal e disponibilize a imagem no grupo de WhatsApp para que os alunos possam pensar sobre ele. Peça que tentem resolver a atividade em três momentos. No primeiro momento pensando sozinho sobre a situação proposta e anotar todas as suas estratégias de cálculo. No segundo momento, eles deverão pedir a um dos seus familiares que tente resolver a situação problema e compartilhar com o aluno como ele pensou. E, para o terceiro momento, o aluno e seu familiar devem discutir uma estratégia conjunta ou validar uma feita por eles individualmente. Oriente-os a filmar ou fotografar as suas estratégias e respostas para compartilhar com o professor e a turma no momento da discussão das soluções.
Discussão das soluções
A discussão das soluções da atividade é uma etapa importantíssima da aula. É o momento de justificar as estratégias e respostas usadas para a resolução do problema proposto na atividade principal. Os alunos devem postar seus vídeos ou fotografias para compartilharem suas respostas em um ambiente de interação como WhatsApp ou Google Sala de Aula, por exemplo, ou ainda organize um powerpoint com algumas soluções trazidas pelos alunos. A intenção é formar um painel de soluções e promover uma discussão rica e estimuladora entre os alunos e professor. Neste momento estimule a turma a falar (usando a ferramenta de áudio ou vídeo) como pensou para resolver o problema. Lance perguntas para guiar a turma nas discussões:
- O que acontece com o valor da distância entre os dois pontos, após ser usada essa escala?
- Qual a diferença entre transformar uma medida real para uma medida no mapa e transformar uma medida do mapa em uma medida real?
Estimule a turma a perceber que, para conhecer uma solução, podemos seguir por diversos caminhos, e que o erro é uma importante ferramenta para o ensino-aprendizagem, combatendo a valorização excessiva da resposta certa.
Convite às famílias
A participação das famílias no processo de aprendizagem é de grande importância para o aluno. Porém, ressaltamos que os pais não são professores de matemática e muitos estão ocupados com outras funções em casa. Portanto, indicamos a participação das famílias no compartilhamento e discussão de possíveis soluções para os problemas propostos.
Este plano de aula foi elaborado pelo Time de Autores NOVA ESCOLA
Autor: Luiz Filipe Trovão
Mentor: Ferdinando Caíque Genghini Dantas Lobo
Especialista: Luciana Maria Tenuta de Freitas
Habilidade da BNCC
EF07MA06 - Reconhecer que as resoluções de um grupo de problemas que têm a mesma estrutura podem ser obtidas utilizando os mesmo procedimentos.
EF07MA08 - Comparar e ordenar frações associadas às ideias de partes de inteiros, resultado da divisão, razão e operador.
EF07MA09 - Utilizar, na resolução de problemas, a associação entre razão e fração, como a fração 2/3 para expressar a razão de duas partes de uma grandeza para três partes da mesma ou três partes de outra grandeza.
Objetivos específicos
- Compreender frações como razão entre duas grandezas;
- Associar o conceito de escala a ideia de fração.
Conceito-chave
Escala como razão entre duas grandezas.
Recursos necessários
Lápis, borracha e caderno.











