Atividade principal
Plano de Aula
Plano de aula: Resolver Problemas Usando Congruência de Triângulos
Plano 7 de uma sequência de 10 planos. Veja todos os planos sobre Transformações isométricas e congruência de triângulos
Descrição
Este plano de aula foi elaborado pelo Time de Autores NOVA ESCOLA
Autora: Renata Akemi Maekawa
Mentor: Fabricio Eduardo Ferreira
Especialista de área: Pricilla Cerqueira
Habilidade da BNCC
(EF08MA12) Demonstrar propriedades de quadriláteros por meio da identificação da congruência de triângulos.
Objetivos específicos
- Comparar triângulos utilizando critérios de congruência de triângulos para determinar medidas de lados e ângulos desconhecidas.
- Utilizar a propriedade em relação à soma dos ângulos internos de um triângulo para obter informações que permitirão verificar congruência entre triângulos.
- Compreender quando não é possível garantir a congruência entre triângulos.
Conceito-chave
Critérios de congruência de triângulos
Recursos necessários
- Fichas impressas.
- Projetor (se possível)
Habilidades BNCC:
Objetivos de aprendizagem
- Comparar triângulos utilizando critérios de congruência de triângulos para determinar medidas de lados e ângulos desconhecidas.
- Utilizar a propriedade em relação à soma dos ângulos internos de um triângulo para obter informações que permitirão verificar congruência entre triângulos.
- Compreender quando não é possível garantir a congruência entre triângulos.
Resumo da Aula
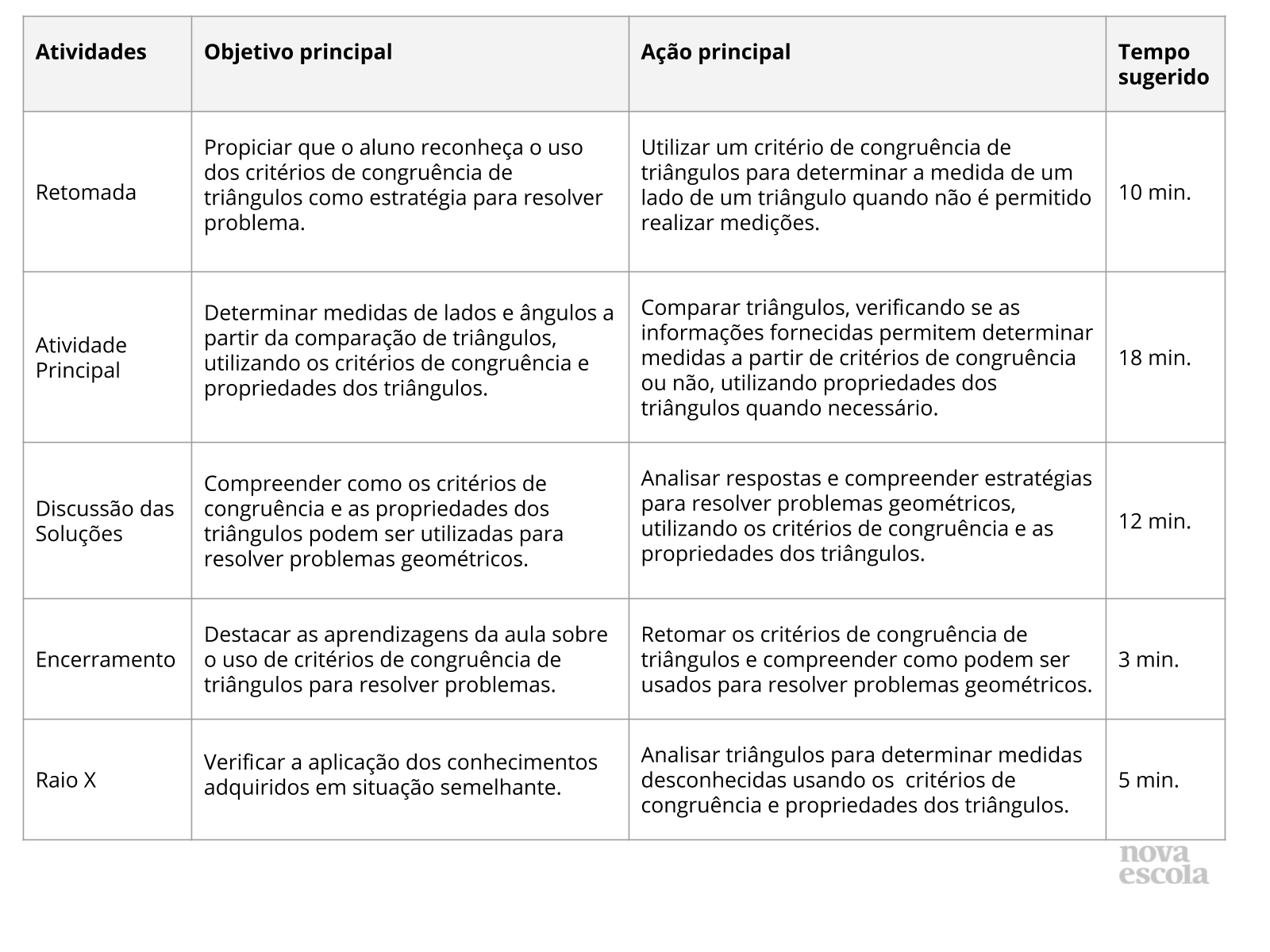
Orientações:Este slide não é um substituto para as anotações para o professor e não deve ser apresentado para os alunos. Trata-se apenas de um resumo da proposta para apoiá-lo na aplicação do plano em sala de aula.
Orientação: Leia atentamente o plano inteiro e as anotações para o professor. Busque antecipar quais questões podem surgir com a sua turma e preveja adequações ao nível em que seus alunos estão.
Compartilhe o objetivo da aula com os alunos antes de aplicar proposta.
Na aba “Sobre o plano”, confira os conhecimentos que sua turma já deve dominar para seguir essa proposta.
Se quiser salvar o plano no seu computador, faça download dos slides na aba “Materiais complementares”. Você também pode imprimi-lo clicando no botão “imprimir”.
Objetivo

Tempo sugerido: 2 minutos.
Orientação: Projete ou leia o objetivo para a turma.
Propósito: Compartilhar o objetivo da aula.
Retomada
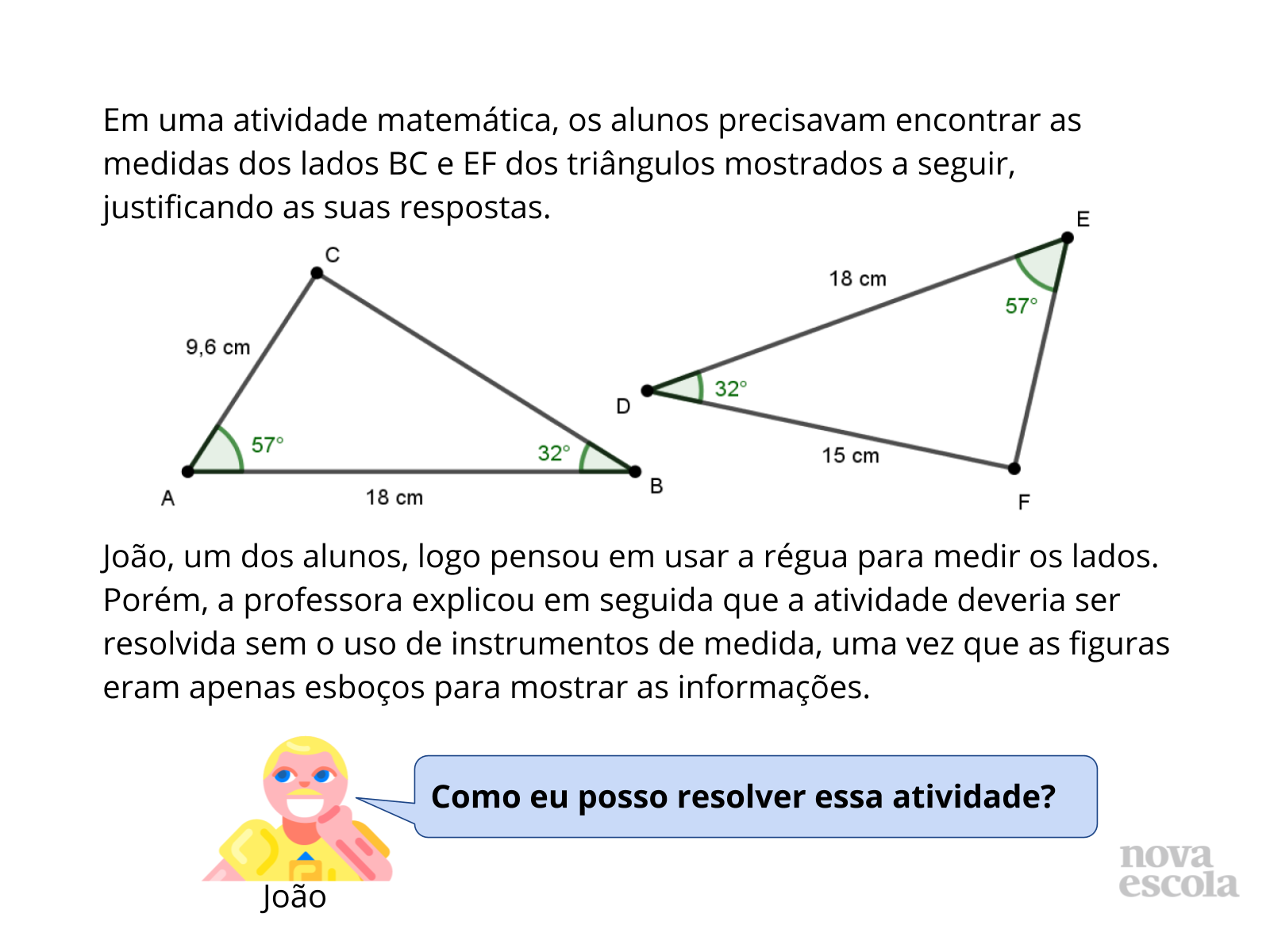
Tempo sugerido: 10 minutos (slides 3 e 4).
Orientações: Inicie a aula projetando a atividade ou entregue cópias da atividade para os alunos. Leia o enunciado para os alunos, organize-os em duplas heterogêneas e solicite que eles pensem na resposta e a anotem em seus cadernos. Circule pela sala para verificar as respostas dos alunos. Em seguida, abra para que os alunos compartilhem suas respostas, iniciando preferencialmente por uma resposta incorreta ou uma resposta sem a justificativa. Discuta com a classe quais justificativas matemáticas eles podem usar para determinar as medidas dos lados desconhecidos. Nessa atividade, é importante que os alunos utilizem um critério de congruência de triângulos para comparar os triângulos e determinar as medidas a partir da definição de congruência.
Você pode usar o slide 4 para apoiar a formalização da resposta após o compartilhamento das respostas dos alunos. Nesse slide, os lados e ângulos congruentes estão destacados com a mesma cor para facilitar a visualização.
Propósito: Propiciar que os alunos trabalhem com uma atividade que demanda o uso dos critérios de congruência de triângulos em sua resolução.
Discuta com a Turma:
- Se não podemos medir, que estratégias podemos utilizar para resolver a atividade?
- O que um critério de congruência de triângulos garante? Como posso utilizá-lo nesse caso?
- Se houvesse apenas um dos triângulos na atividade, seria possível resolvê-la?
- Materiais complementares:
Retomada
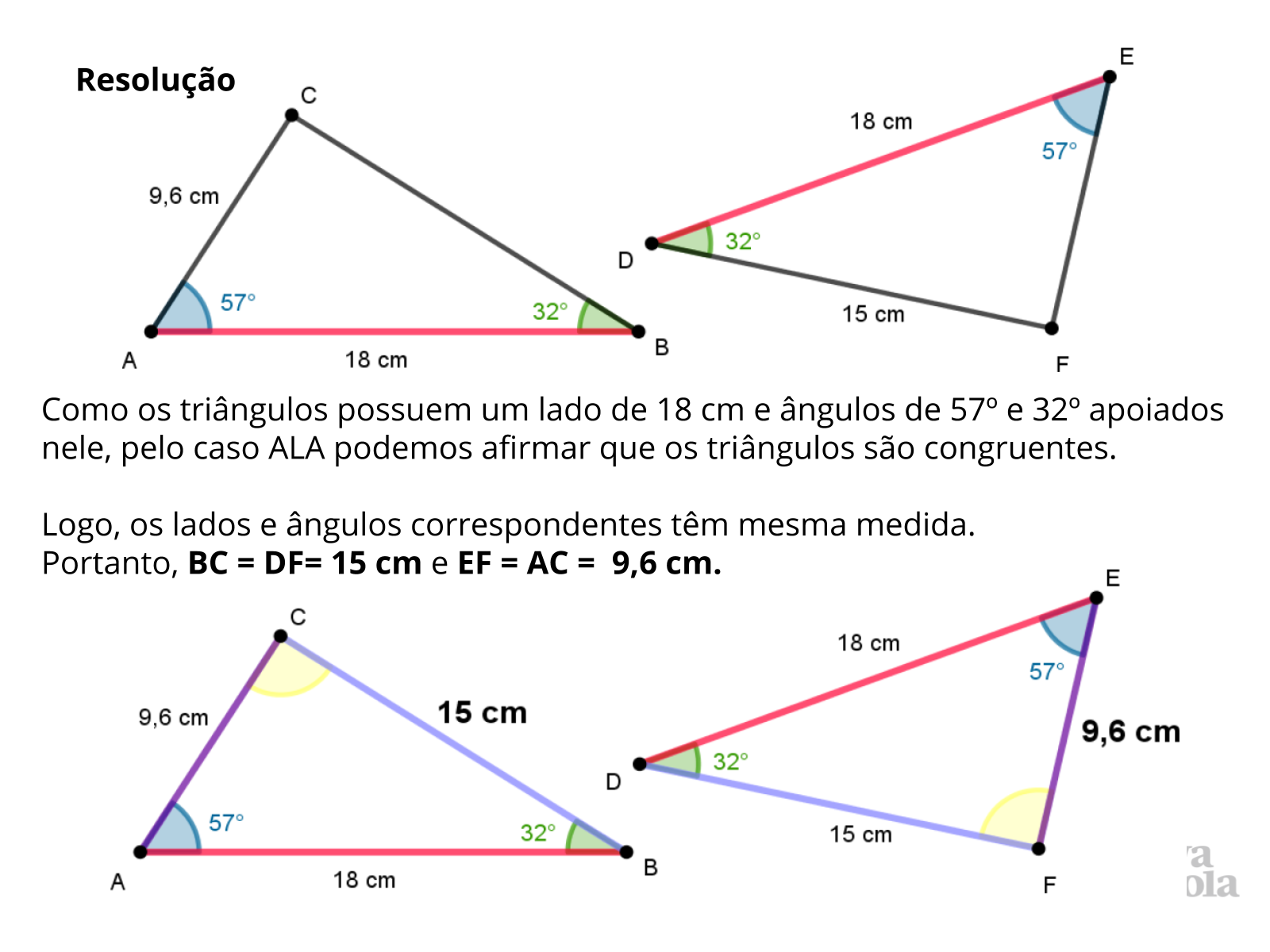
Tempo sugerido: 10 minutos (slides 3 e 4).
Orientações: Inicie a aula projetando a atividade ou entregue cópias da atividade para os alunos. Leia o enunciado para os alunos, organize-os em duplas heterogêneas e solicite que eles pensem na resposta e a anotem em seus cadernos. Circule pela sala para verificar as respostas dos alunos. Em seguida, abra para que os alunos compartilhem suas respostas, iniciando preferencialmente por uma resposta incorreta ou uma resposta sem a justificativa. Discuta com a classe quais justificativas matemáticas eles podem usar para determinar as medidas dos lados desconhecidos. Nessa atividade, é importante que os alunos utilizem um critério de congruência de triângulos para comparar os triângulos e determinar as medidas a partir da definição de congruência.
Você pode usar o slide 4 para apoiar a formalização da resposta após o compartilhamento das respostas dos alunos. Nesse slide, os lados e ângulos congruentes estão destacados com a mesma cor para facilitar a visualização.
Propósito: Propiciar que os alunos trabalhem com uma atividade que demanda o uso dos critérios de congruência de triângulos em sua resolução.
Discuta com a Turma:
- Se não podemos medir, que estratégias podemos utilizar para resolver a atividade?
- O que um critério de congruência de triângulos garante? Como posso utilizá-lo nesse caso?
- Se houvesse apenas um dos triângulos na atividade, seria possível resolvê-la?
Atividade Principal
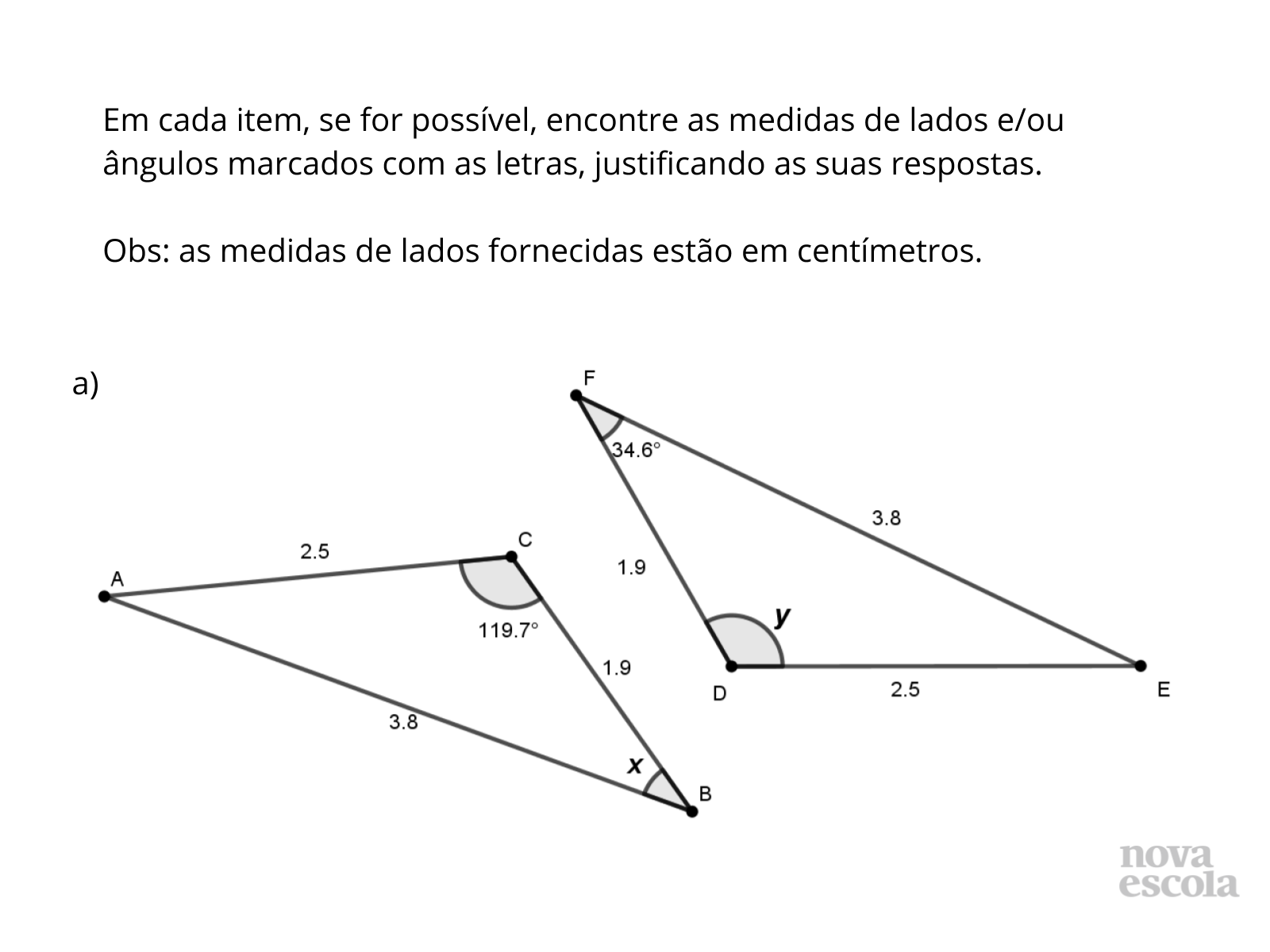
Tempo sugerido: 18 minutos (slides 5 a 7).
Orientações: Projete esta atividade ou imprima e entregue uma cópia para cada aluno. Reúna os alunos em quartetos, juntando duas duplas que trabalharam juntas no momento anterior. Proponha que eles resolvam os itens primeiramente na dupla para depois discutir as respostas no grupo. Lembre-os que todos devem registrar as respostas em seus cadernos e que devem debater as respostas até que todos os membros do grupo concordem.
Circule pela sala para observar como os alunos estão resolvendo o problema, sem informar os grupos se a resposta obtida por eles está correta ou não.
Se algum grupo terminar, peça que retome os itens e verifique se conseguiu descobrir a medida de mais algum ângulo ou mais algum lado que não está marcado com letras.
Propósito: Incentivar que os alunos comparem triângulos utilizando critérios de congruência de triângulos e propriedade dos triângulos em relação a soma dos ângulos internos para determinar medidas desconhecidas.
Materiais complementares:
Atividade Principal
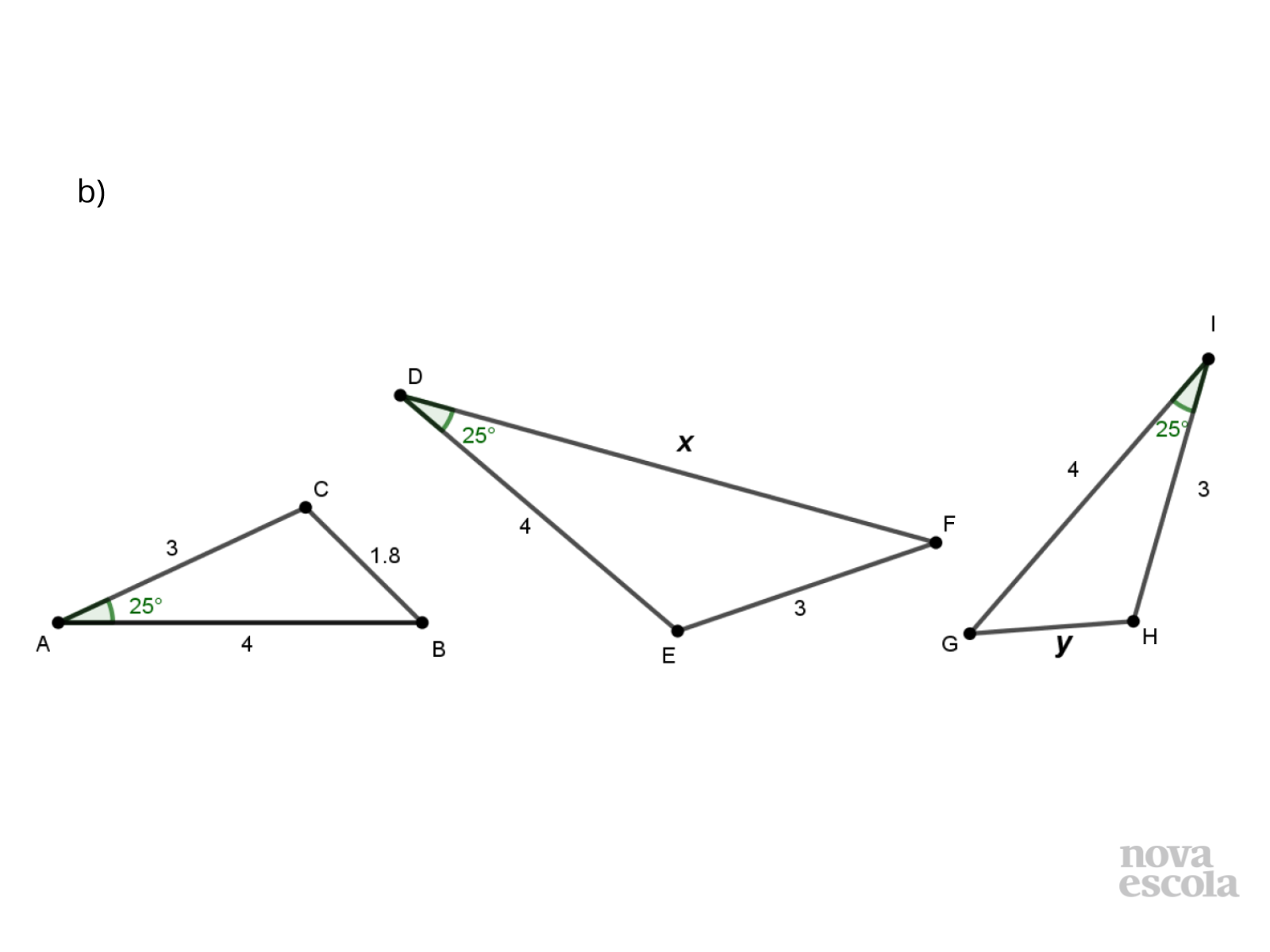
Tempo sugerido: 18 minutos (slides 5 a 7).
Orientações: Projete esta atividade ou imprima e entregue uma cópia para cada aluno. Reúna os alunos em quartetos, juntando duas duplas que trabalharam juntas no momento anterior. Proponha que eles resolvam os itens primeiramente na dupla para depois discutir as respostas no grupo. Lembre-os que todos devem registrar as respostas em seus cadernos e que devem debater as respostas até que todos os membros do grupo concordem.
Circule pela sala para observar como os alunos estão resolvendo o problema, sem informar os grupos se a resposta obtida por eles está correta ou não.
Se algum grupo terminar, peça que retome os itens e verifique se conseguiu descobrir a medida de mais algum ângulo ou mais algum lado que não está marcado com letras.
Propósito: Incentivar que os alunos comparem triângulos utilizando critérios de congruência de triângulos e propriedade dos triângulos em relação a soma dos ângulos internos para determinar medidas desconhecidas.
Atividade Principal
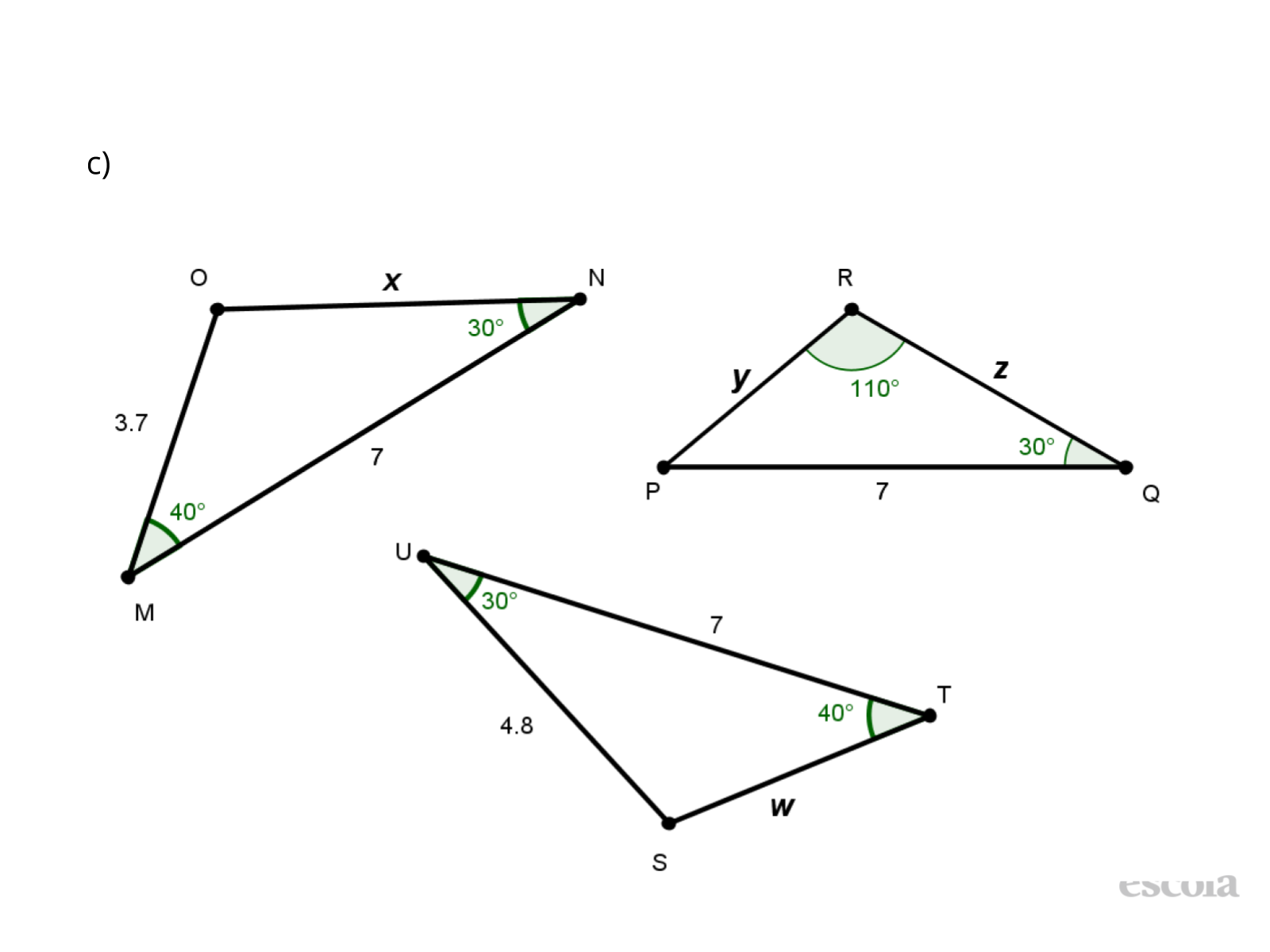
Tempo sugerido: 18 minutos (slides 5 a 7).
Orientações: Projete esta atividade ou imprima e entregue uma cópia para cada aluno. Reúna os alunos em quartetos, juntando duas duplas que trabalharam juntas no momento anterior. Proponha que eles resolvam os itens primeiramente na dupla para depois discutir as respostas no grupo. Lembre-os que todos devem registrar as respostas em seus cadernos e que devem debater as respostas até que todos os membros do grupo concordem.
Circule pela sala para observar como os alunos estão resolvendo o problema, sem informar os grupos se a resposta obtida por eles está correta ou não.
Se algum grupo terminar, peça que retome os itens e verifique se conseguiu descobrir a medida de mais algum ângulo ou mais algum lado que não está marcado com letras.
Propósito: Incentivar que os alunos comparem triângulos utilizando critérios de congruência de triângulos e propriedade dos triângulos em relação a soma dos ângulos internos para determinar medidas desconhecidas.
Discussão das Soluções
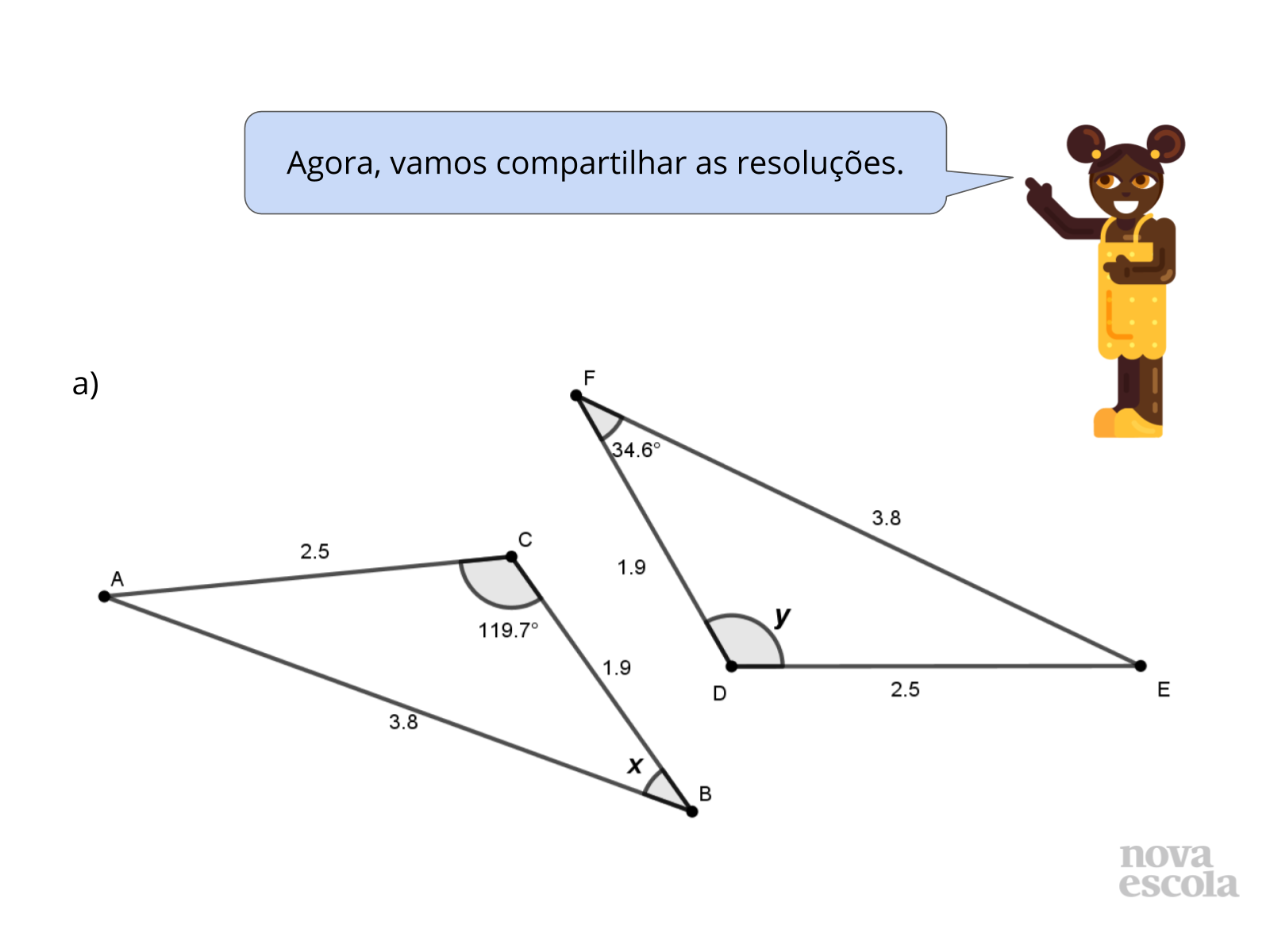
Tempo sugerido: 12 minutos (slides 8 a 13).
Orientações: Explique que os itens serão discutidos na ordem. Para cada item, solicite que os grupos compartilhem os valores encontrados e as justificativas e também digam quais medidas não podem ser determinadas, explicando o porquê. É importante que as diferentes respostas, se existirem, apareçam nesse momento de compartilhamento (a observação feita das resoluções dos alunos no momento anterior é importante, pois, a partir dela o professor pode selecionar as resoluções que potencializarão a discussão, lembrando que as discussões sobre os erros e motivos que os originaram também são essenciais). Verifique também se algum outro grupo deseja complementar a resposta dada por outro colega. Abra para que a turma discuta a solução. Nessa etapa da aula, é essencial que os critérios de congruência de triângulos apareçam nas justificativas das medidas determinadas e também que se explore os motivos que levam a impossibilidade de descobrir alguns valores. Para cada item, há um slide com a reprodução dos triângulos da atividade para apoiar a discussão. Em seguida, há um slide com lados e ângulos congruentes destacados com cores e a formalização da resposta da questão. Utilize os slides com as respostas se julgar necessário (o slide deve ser exibido após os alunos terem discutido as resoluções e terem chegado a um consenso da resposta). É importante que os alunos façam registros em seus cadernos das respostas e justificativas.
O item c é o mais desafiador, pois exige que os alunos utilizem as propriedades dos triângulos em relação à soma dos ângulos internos para resolvê-lo. É possível que os grupos determinem as medidas de x e w desse item, mas considerem que y e z não são determináveis. Se isso ocorrer, informe os grupos que essas duas medidas também podem ser determinadas e peça para que eles se reúnam, determinem quais são as medidas e busquem uma forma de justificar, pelos critérios de congruência. Por fim, abra novamente para o discussão coletiva da resposta.
Propósito: Propiciar que os alunos resolvam problemas geométricos, analisando explicações dos colegas e justificando por meio dos critérios de congruência de triângulos e propriedades dos triângulos.
Discuta com a Turma:
- Os critérios de congruência de triângulos servem para justificar as medidas de lados e ângulos?
- Seria possível determinar as medidas se algum dos triângulos não fosse fornecido? Por quê?
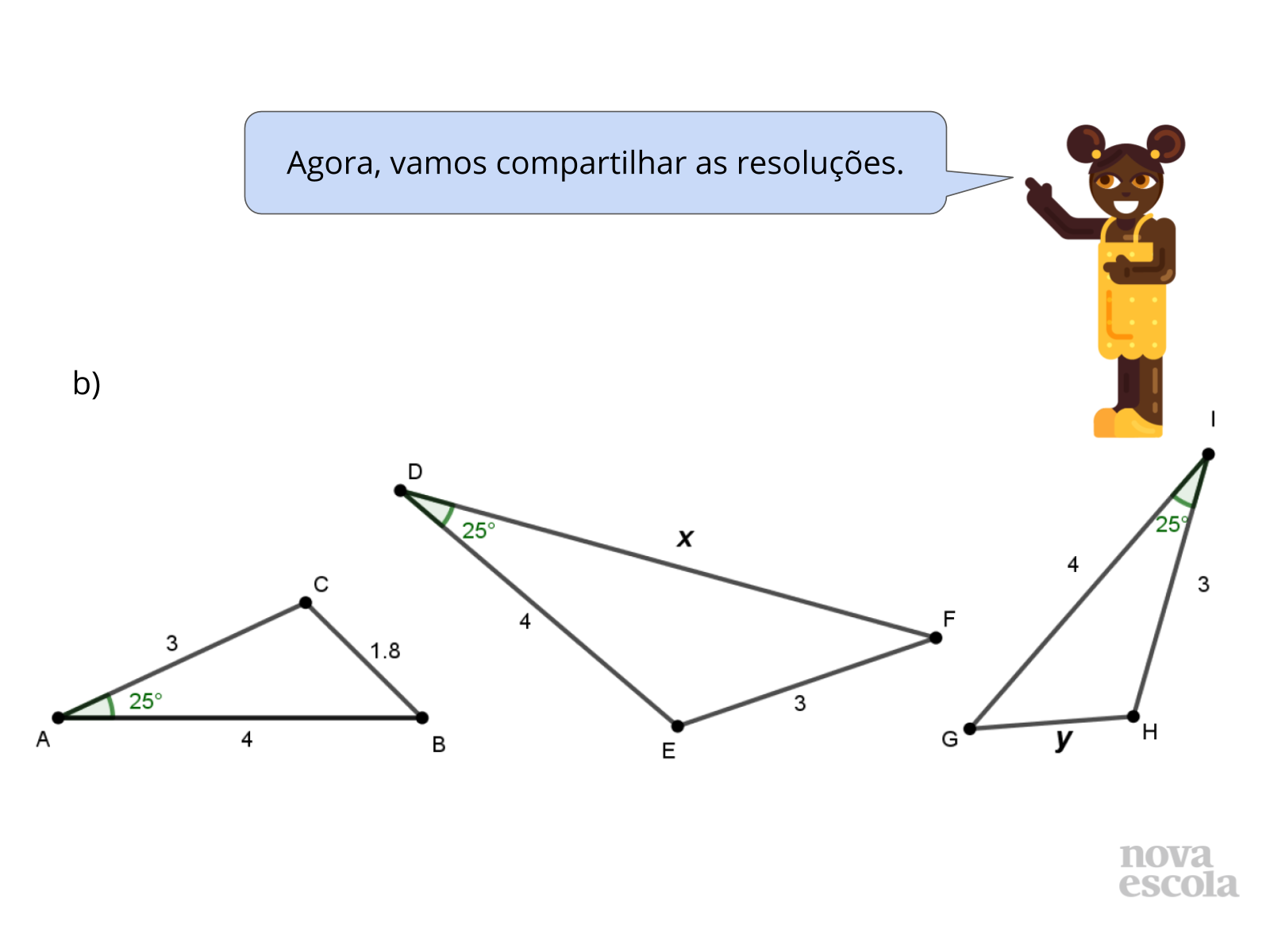
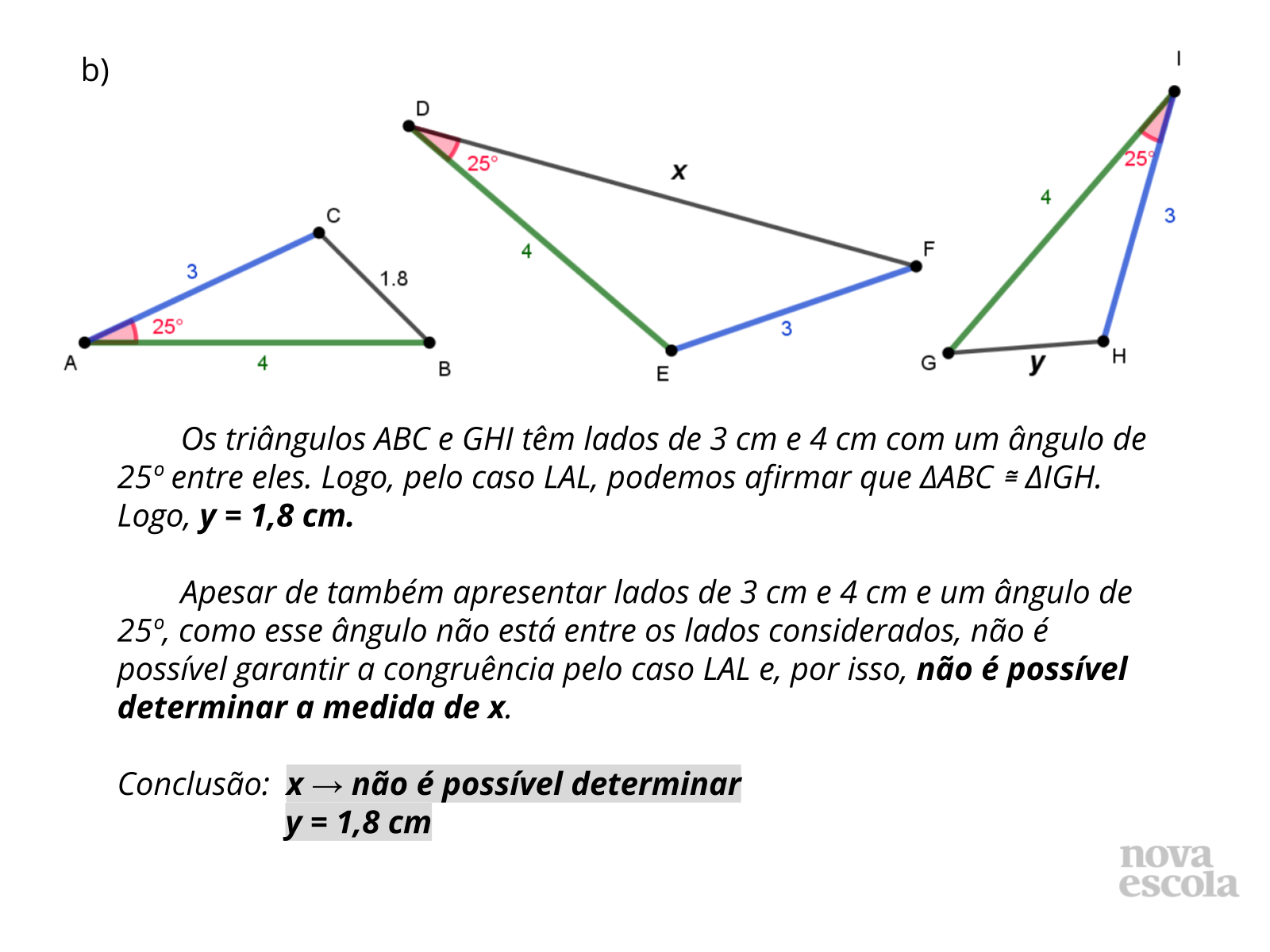
- No item b, todos os triângulos têm lados de 4 cm, 3 cm e um ângulo de 25º. Por que não é possível determinar a medida x?
- Qual é a propriedade em relação à soma dos ângulos internos de um triângulo? Como ela pode ajudar a resolver problemas de congruência de triângulos?
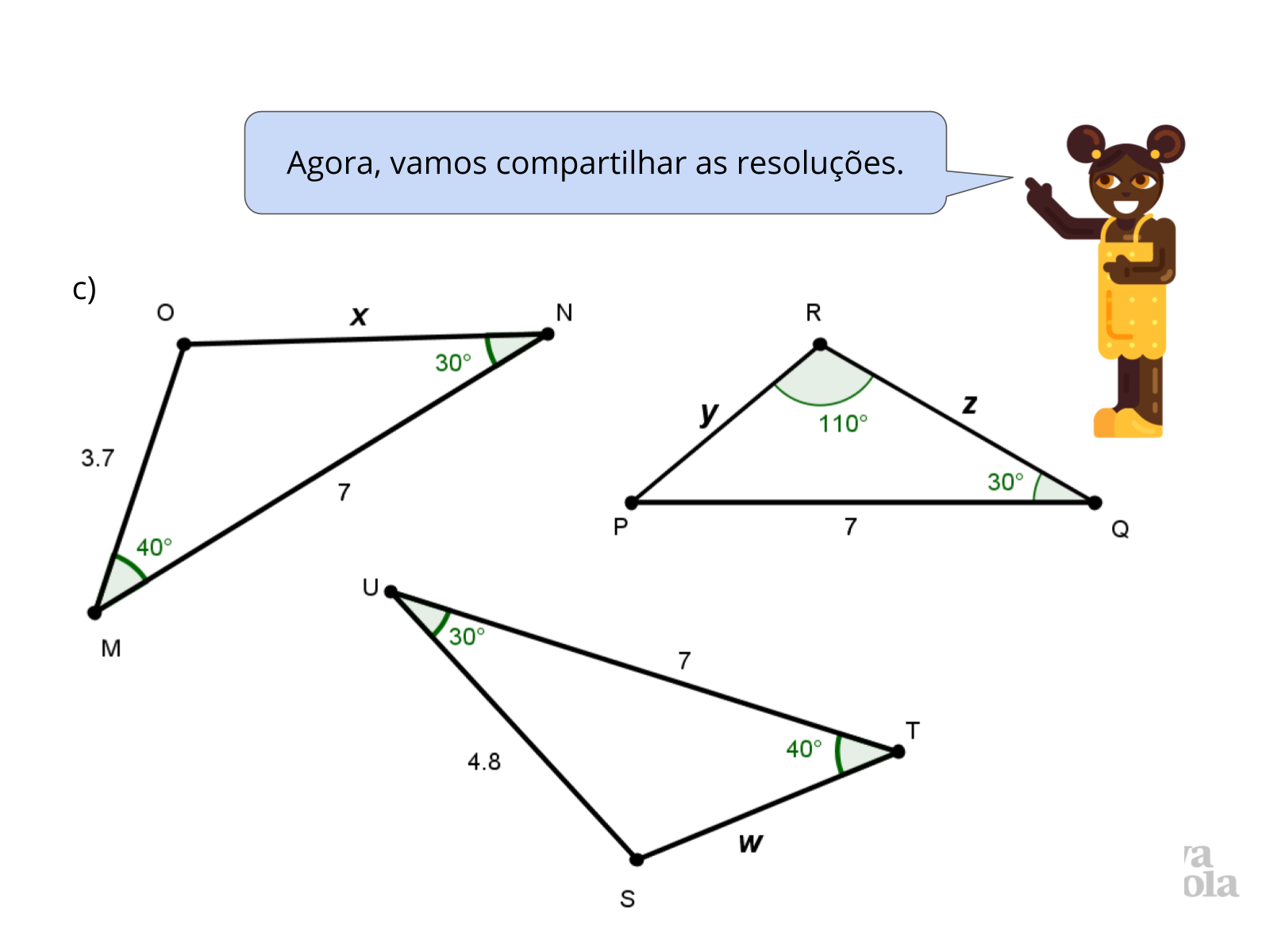
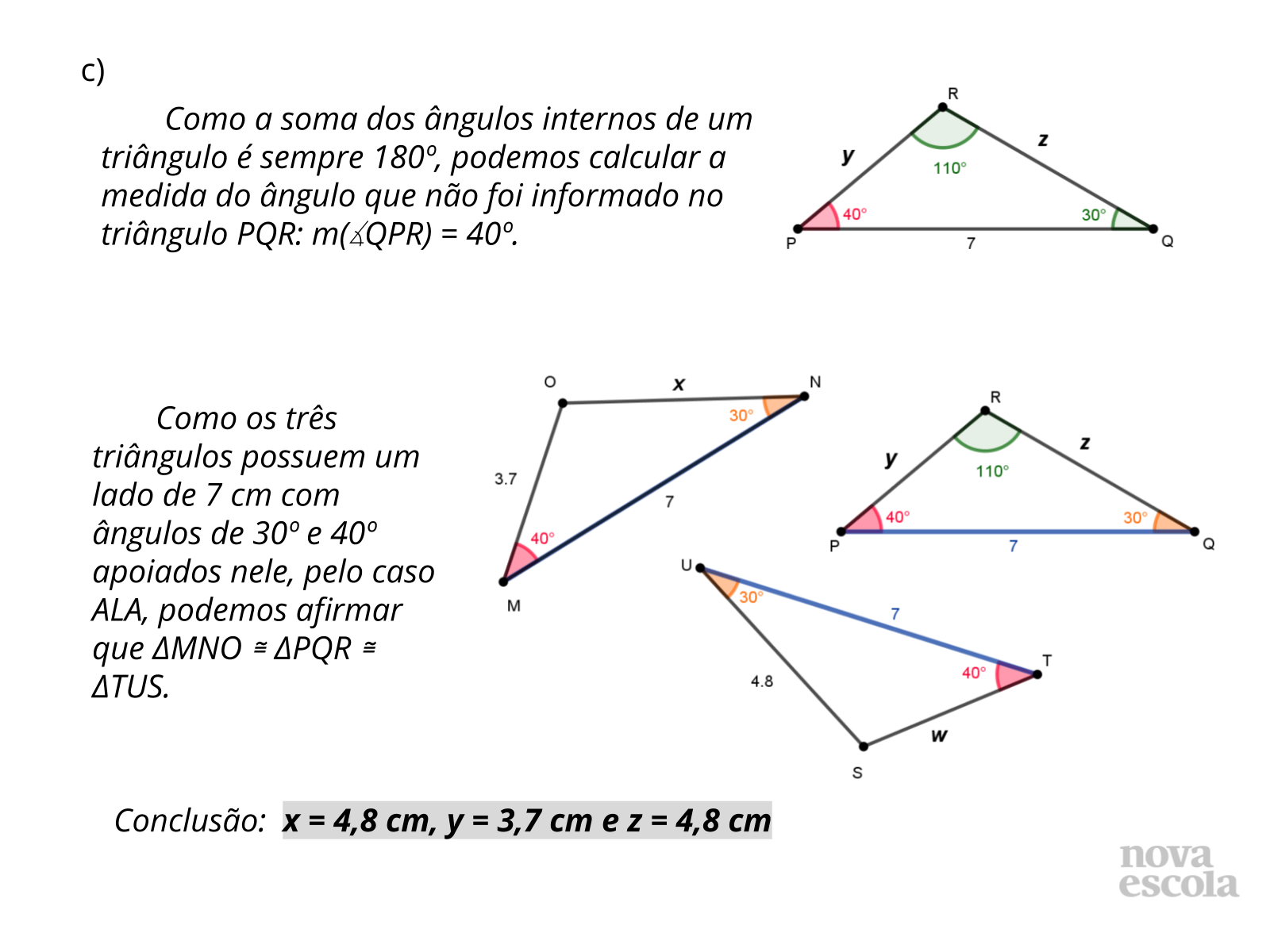
- No item c, os lados de 3,7 cm e 4,8 cm estão marcados com letras no triângulo PQR. Como podemos saber qual desses correponde a y e qual correspnde a z? Posso escolher?
Discussão das Soluções
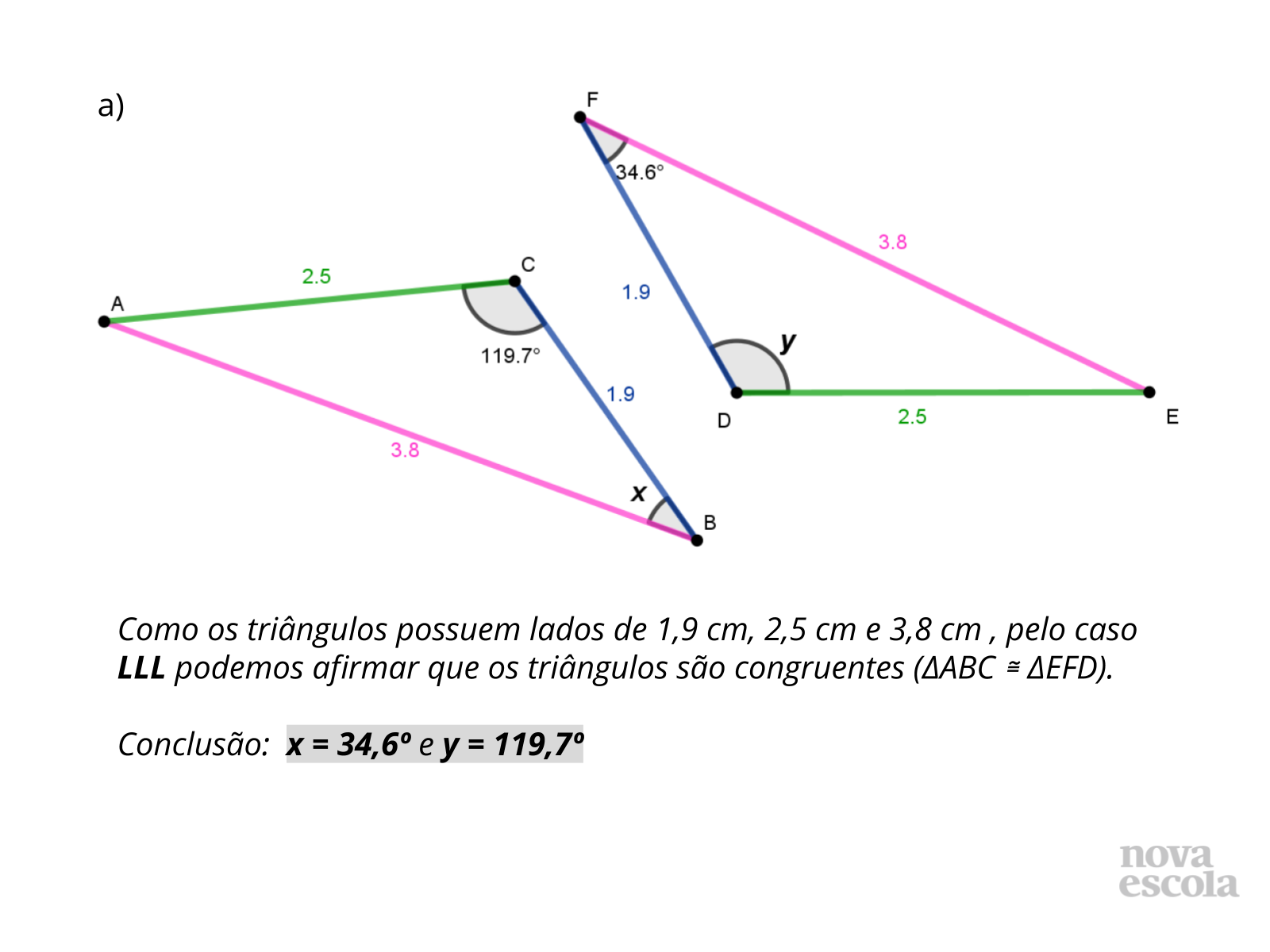
Tempo sugerido: 12 minutos (slides 8 a 13).
Orientações: Explique que os itens serão discutidos na ordem. Para cada item, solicite que os grupos compartilhem os valores encontrados e as justificativas e também digam quais medidas não podem ser determinadas, explicando o porquê. É importante que as diferentes respostas, se existirem, apareçam nesse momento de compartilhamento (a observação feita das resoluções dos alunos no momento anterior é importante, pois, a partir dela o professor pode selecionar as resoluções que potencializarão a discussão, lembrando que as discussões sobre os erros e motivos que os originaram também são essenciais). Verifique também se algum outro grupo deseja complementar a resposta dada por outro colega. Abra para que a turma discuta a solução. Nessa etapa da aula, é essencial que os critérios de congruência de triângulos apareçam nas justificativas das medidas determinadas e também que se explore os motivos que levam a impossibilidade de descobrir alguns valores. Para cada item, há um slide com a reprodução dos triângulos da atividade para apoiar a discussão. Em seguida, há um slide com lados e ângulos congruentes destacados com cores e a formalização da resposta da questão. Utilize os slides com as respostas se julgar necessário (o slide deve ser exibido após os alunos terem discutido as resoluções e terem chegado a um consenso da resposta). É importante que os alunos façam registros em seus cadernos das respostas e justificativas.
O item c é o mais desafiador, pois exige que os alunos utilizem as propriedades dos triângulos em relação à soma dos ângulos internos para resolvê-lo. É possível que os grupos determinem as medidas de x e w desse item, mas considerem que y e z não são determináveis. Se isso ocorrer, informe os grupos que essas duas medidas também podem ser determinadas e peça para que eles se reúnam, determinem quais são as medidas e busquem uma forma de justificar, pelos critérios de congruência. Por fim, abra novamente para o discussão coletiva da resposta.
Propósito: Propiciar que os alunos resolvam problemas geométricos, analisando explicações dos colegas e justificando por meio dos critérios de congruência de triângulos e propriedades dos triângulos.
Discuta com a Turma:
- Os critérios de congruência de triângulos servem para justificar as medidas de lados e ângulos?
- Seria possível determinar as medidas se algum dos triângulos não fosse fornecido? Por quê?
- No item b, todos os triângulos têm lados de 4 cm, 3 cm e um ângulo de 25º. Por que não é possível determinar a medida x?
- Qual é a propriedade em relação à soma dos ângulos internos de um triângulo? Como ela pode ajudar a resolver problemas de congruência de triângulos?
- No item c, os lados de 3,7 cm e 4,8 cm estão marcados com letras no triângulo PQR. Como podemos saber qual desses correponde a y e qual correspnde a z? Posso escolher?
Discussão das Soluções
Tempo sugerido: 12 minutos (slides 8 a 13).
Orientações: Explique que os itens serão discutidos na ordem. Para cada item, solicite que os grupos compartilhem os valores encontrados e as justificativas e também digam quais medidas não podem ser determinadas, explicando o porquê. É importante que as diferentes respostas, se existirem, apareçam nesse momento de compartilhamento (a observação feita das resoluções dos alunos no momento anterior é importante, pois, a partir dela o professor pode selecionar as resoluções que potencializarão a discussão, lembrando que as discussões sobre os erros e motivos que os originaram também são essenciais). Verifique também se algum outro grupo deseja complementar a resposta dada por outro colega. Abra para que a turma discuta a solução. Nessa etapa da aula, é essencial que os critérios de congruência de triângulos apareçam nas justificativas das medidas determinadas e também que se explore os motivos que levam a impossibilidade de descobrir alguns valores. Para cada item, há um slide com a reprodução dos triângulos da atividade para apoiar a discussão. Em seguida, há um slide com lados e ângulos congruentes destacados com cores e a formalização da resposta da questão. Utilize os slides com as respostas se julgar necessário (o slide deve ser exibido após os alunos terem discutido as resoluções e terem chegado a um consenso da resposta). É importante que os alunos façam registros em seus cadernos das respostas e justificativas.
O item c é o mais desafiador, pois exige que os alunos utilizem as propriedades dos triângulos em relação à soma dos ângulos internos para resolvê-lo. É possível que os grupos determinem as medidas de x e w desse item, mas considerem que y e z não são determináveis. Se isso ocorrer, informe os grupos que essas duas medidas também podem ser determinadas e peça para que eles se reúnam, determinem quais são as medidas e busquem uma forma de justificar, pelos critérios de congruência. Por fim, abra novamente para o discussão coletiva da resposta.
Propósito: Propiciar que os alunos resolvam problemas geométricos, analisando explicações dos colegas e justificando por meio dos critérios de congruência de triângulos e propriedades dos triângulos.
Discuta com a Turma:
- Os critérios de congruência de triângulos servem para justificar as medidas de lados e ângulos?
- Seria possível determinar as medidas se algum dos triângulos não fosse fornecido? Por quê?
- No item b, todos os triângulos têm lados de 4 cm, 3 cm e um ângulo de 25º. Por que não é possível determinar a medida x?
- Qual é a propriedade em relação à soma dos ângulos internos de um triângulo? Como ela pode ajudar a resolver problemas de congruência de triângulos?
- No item c, os lados de 3,7 cm e 4,8 cm estão marcados com letras no triângulo PQR. Como podemos saber qual desses correponde a y e qual correspnde a z? Posso escolher?
Discussão das Soluções
Tempo sugerido: 12 minutos (slides 8 a 13).
Orientações: Explique que os itens serão discutidos na ordem. Para cada item, solicite que os grupos compartilhem os valores encontrados e as justificativas e também digam quais medidas não podem ser determinadas, explicando o porquê. É importante que as diferentes respostas, se existirem, apareçam nesse momento de compartilhamento (a observação feita das resoluções dos alunos no momento anterior é importante, pois, a partir dela o professor pode selecionar as resoluções que potencializarão a discussão, lembrando que as discussões sobre os erros e motivos que os originaram também são essenciais). Verifique também se algum outro grupo deseja complementar a resposta dada por outro colega. Abra para que a turma discuta a solução. Nessa etapa da aula, é essencial que os critérios de congruência de triângulos apareçam nas justificativas das medidas determinadas e também que se explore os motivos que levam a impossibilidade de descobrir alguns valores. Para cada item, há um slide com a reprodução dos triângulos da atividade para apoiar a discussão. Em seguida, há um slide com lados e ângulos congruentes destacados com cores e a formalização da resposta da questão. Utilize os slides com as respostas se julgar necessário (o slide deve ser exibido após os alunos terem discutido as resoluções e terem chegado a um consenso da resposta). É importante que os alunos façam registros em seus cadernos das respostas e justificativas.
O item c é o mais desafiador, pois exige que os alunos utilizem as propriedades dos triângulos em relação à soma dos ângulos internos para resolvê-lo. É possível que os grupos determinem as medidas de x e w desse item, mas considerem que y e z não são determináveis. Se isso ocorrer, informe os grupos que essas duas medidas também podem ser determinadas e peça para que eles se reúnam, determinem quais são as medidas e busquem uma forma de justificar, pelos critérios de congruência. Por fim, abra novamente para o discussão coletiva da resposta.
Propósito: Propiciar que os alunos resolvam problemas geométricos, analisando explicações dos colegas e justificando por meio dos critérios de congruência de triângulos e propriedades dos triângulos.
Discuta com a Turma:
- Os critérios de congruência de triângulos servem para justificar as medidas de lados e ângulos?
- Seria possível determinar as medidas se algum dos triângulos não fosse fornecido? Por quê?
- No item b, todos os triângulos têm lados de 4 cm, 3 cm e um ângulo de 25º. Por que não é possível determinar a medida x?
- Qual é a propriedade em relação à soma dos ângulos internos de um triângulo? Como ela pode ajudar a resolver problemas de congruência de triângulos?
- No item c, os lados de 3,7 cm e 4,8 cm estão marcados com letras no triângulo PQR. Como podemos saber qual desses correponde a y e qual correspnde a z? Posso escolher?
Discussão das Soluções
Tempo sugerido: 12 minutos (slides 8 a 13).
Orientações: Explique que os itens serão discutidos na ordem. Para cada item, solicite que os grupos compartilhem os valores encontrados e as justificativas e também digam quais medidas não podem ser determinadas, explicando o porquê. É importante que as diferentes respostas, se existirem, apareçam nesse momento de compartilhamento (a observação feita das resoluções dos alunos no momento anterior é importante, pois, a partir dela o professor pode selecionar as resoluções que potencializarão a discussão, lembrando que as discussões sobre os erros e motivos que os originaram também são essenciais). Verifique também se algum outro grupo deseja complementar a resposta dada por outro colega. Abra para que a turma discuta a solução. Nessa etapa da aula, é essencial que os critérios de congruência de triângulos apareçam nas justificativas das medidas determinadas e também que se explore os motivos que levam a impossibilidade de descobrir alguns valores. Para cada item, há um slide com a reprodução dos triângulos da atividade para apoiar a discussão. Em seguida, há um slide com lados e ângulos congruentes destacados com cores e a formalização da resposta da questão. Utilize os slides com as respostas se julgar necessário (o slide deve ser exibido após os alunos terem discutido as resoluções e terem chegado a um consenso da resposta). É importante que os alunos façam registros em seus cadernos das respostas e justificativas.
O item c é o mais desafiador, pois exige que os alunos utilizem as propriedades dos triângulos em relação à soma dos ângulos internos para resolvê-lo. É possível que os grupos determinem as medidas de x e w desse item, mas considerem que y e z não são determináveis. Se isso ocorrer, informe os grupos que essas duas medidas também podem ser determinadas e peça para que eles se reúnam, determinem quais são as medidas e busquem uma forma de justificar, pelos critérios de congruência. Por fim, abra novamente para o discussão coletiva da resposta.
Propósito: Propiciar que os alunos resolvam problemas geométricos, analisando explicações dos colegas e justificando por meio dos critérios de congruência de triângulos e propriedades dos triângulos.
Discuta com a Turma:
- Os critérios de congruência de triângulos servem para justificar as medidas de lados e ângulos?
- Seria possível determinar as medidas se algum dos triângulos não fosse fornecido? Por quê?
- No item b, todos os triângulos têm lados de 4 cm, 3 cm e um ângulo de 25º. Por que não é possível determinar a medida x?
- Qual é a propriedade em relação à soma dos ângulos internos de um triângulo? Como ela pode ajudar a resolver problemas de congruência de triângulos?
- No item c, os lados de 3,7 cm e 4,8 cm estão marcados com letras no triângulo PQR. Como podemos saber qual desses correponde a y e qual correspnde a z? Posso escolher?
Discussão das Soluções
Tempo sugerido: 12 minutos (slides 8 a 13).
Orientações: Explique que os itens serão discutidos na ordem. Para cada item, solicite que os grupos compartilhem os valores encontrados e as justificativas e também digam quais medidas não podem ser determinadas, explicando o porquê. É importante que as diferentes respostas, se existirem, apareçam nesse momento de compartilhamento (a observação feita das resoluções dos alunos no momento anterior é importante, pois, a partir dela o professor pode selecionar as resoluções que potencializarão a discussão, lembrando que as discussões sobre os erros e motivos que os originaram também são essenciais). Verifique também se algum outro grupo deseja complementar a resposta dada por outro colega. Abra para que a turma discuta a solução. Nessa etapa da aula, é essencial que os critérios de congruência de triângulos apareçam nas justificativas das medidas determinadas e também que se explore os motivos que levam a impossibilidade de descobrir alguns valores. Para cada item, há um slide com a reprodução dos triângulos da atividade para apoiar a discussão. Em seguida, há um slide com lados e ângulos congruentes destacados com cores e a formalização da resposta da questão. Utilize os slides com as respostas se julgar necessário (o slide deve ser exibido após os alunos terem discutido as resoluções e terem chegado a um consenso da resposta). É importante que os alunos façam registros em seus cadernos das respostas e justificativas.
O item c é o mais desafiador, pois exige que os alunos utilizem as propriedades dos triângulos em relação à soma dos ângulos internos para resolvê-lo. É possível que os grupos determinem as medidas de x e w desse item, mas considerem que y e z não são determináveis. Se isso ocorrer, informe os grupos que essas duas medidas também podem ser determinadas e peça para que eles se reúnam, determinem quais são as medidas e busquem uma forma de justificar, pelos critérios de congruência. Por fim, abra novamente para o discussão coletiva da resposta.
Propósito: Propiciar que os alunos resolvam problemas geométricos, analisando explicações dos colegas e justificando por meio dos critérios de congruência de triângulos e propriedades dos triângulos.
Discuta com a Turma:
- Os critérios de congruência de triângulos servem para justificar as medidas de lados e ângulos?
- Seria possível determinar as medidas se algum dos triângulos não fosse fornecido? Por quê?
- No item b, todos os triângulos têm lados de 4 cm, 3 cm e um ângulo de 25º. Por que não é possível determinar a medida x?
- Qual é a propriedade em relação à soma dos ângulos internos de um triângulo? Como ela pode ajudar a resolver problemas de congruência de triângulos?
- No item c, os lados de 3,7 cm e 4,8 cm estão marcados com letras no triângulo PQR. Como podemos saber qual desses correponde a y e qual correspnde a z? Posso escolher?
Encerramento
Tempo sugerido: 3 minutos.
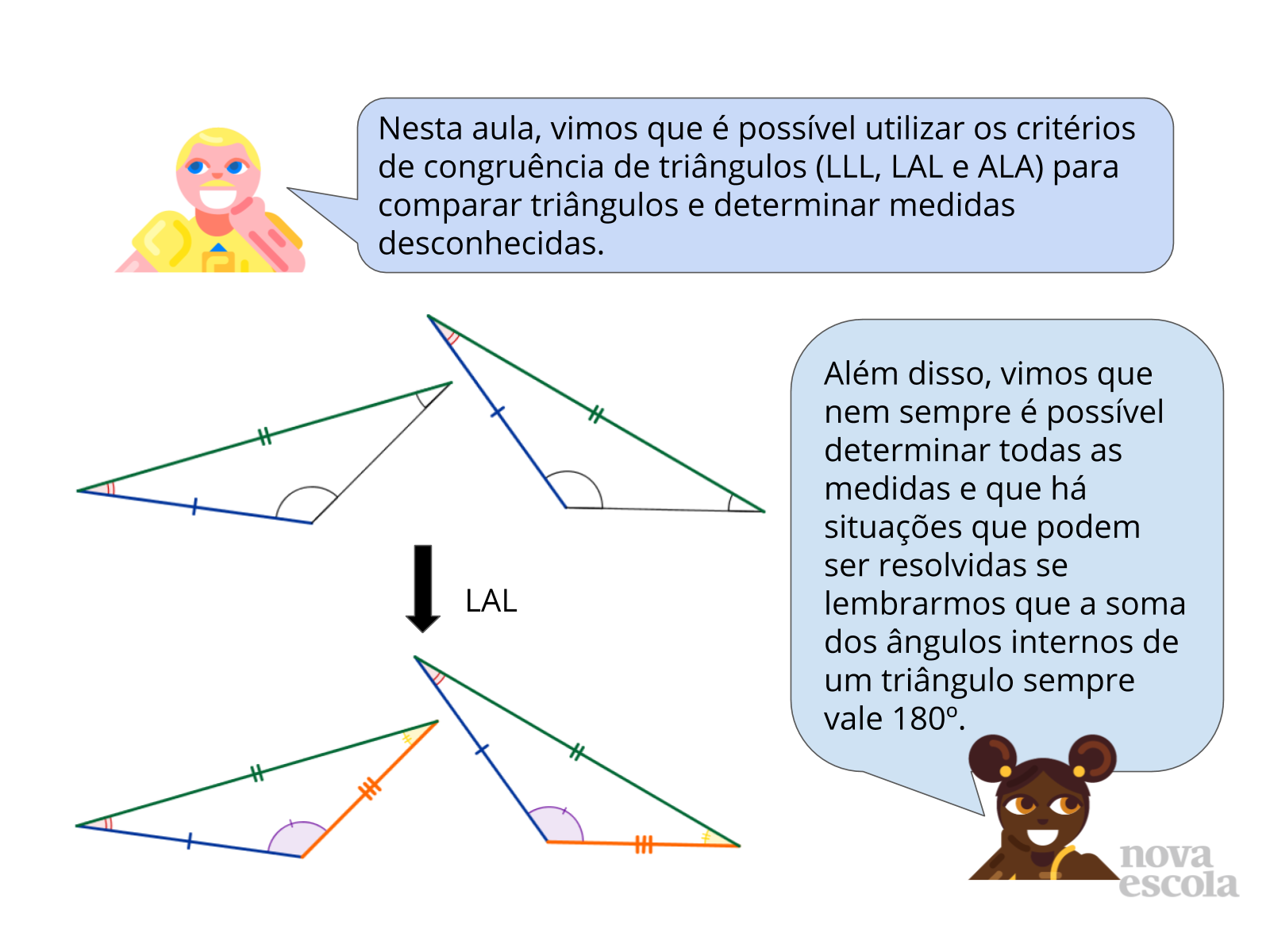
Orientações: Solicite que os alunos digam quais foram os pontos mais importantes trabalhados em aula (antes de exibir o slide). Depois, leia os textos desse slide, ou peça para algum aluno leia para sistematizar as aprendizagens da aula, verificando se algum ponto não havia sido destacado pelos alunos e/ou completando a sistematização da aula com pontos levantados pelos alunos que não estão escritos. Caso os alunos não conheçam, comente sobre a possibilidade de fazer marcas iguais para indicar congruência entre lados ou ângulos, como mostrado na imagem.
Propósito: Retomar as aprendizagens da aula, destacando o uso dos critérios de congruência de triângulos para resolver problemas geométricos.
Raio X
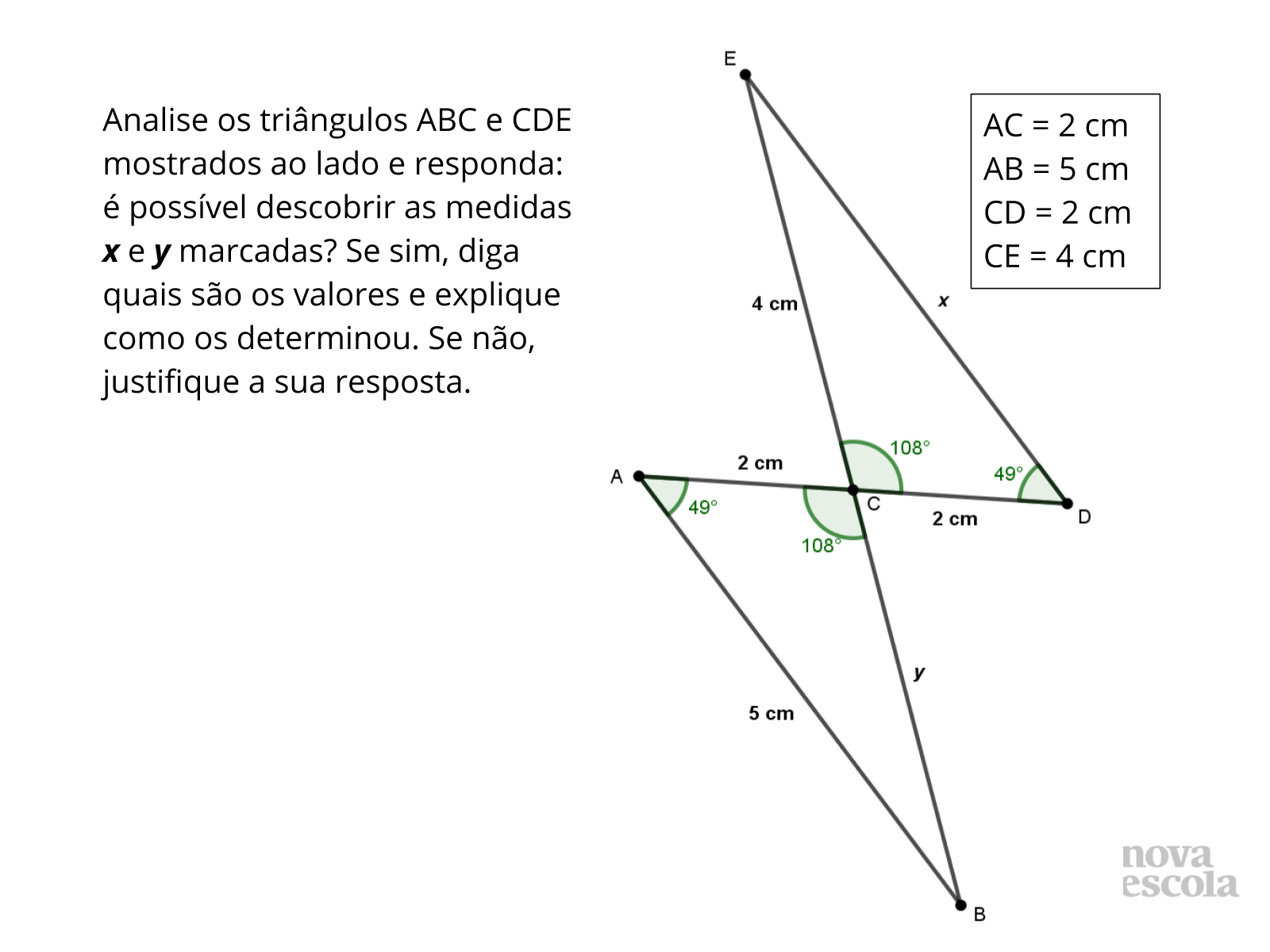
Tempo sugerido: 5 minutos.
Orientações: Projete a atividade ou entregue cópias para os alunos e peça que, individualmente, leiam o enunciado e a realizem a atividade. Circule pela classe para verificar como os alunos estão realizando a tarefa e, caso algum aluno termine, solicite que ele verifique se é possível descobrir a medida dos ângulos não fornecidos dos triângulos. O Raio X é um momento para você avaliar se todos os estudantes conseguiram avançar no conteúdo proposto, então procure identificar e anotar os comentários de cada um. No final, reserve um tempo para um debate coletivo.
Propósito: Verificar se os alunos aplicam os conhecimentos adquiridos numa situação semelhante e avaliar os conhecimentos de cada um a respeito do uso dos critérios de congruência de triângulos para resolver problemas geométricos.
Materiais complementares:
Resolução atividade complementar
Sugestão de adaptação para ensino remoto
Código do plano
MAT8_15GEO07
Recursos
USAR APENAS FERRAMENTAS EM PORTUGUÊS E GRATUITAS
- Necessários: Papel, lápis, WhatsApp
- Opcionais: Messenger Sala de aluno ( https://www.messenger.com/groupcall/LINK:4svjhs7dyZw8zoxm/), Meet, Hangout, Zoom, plataforma da Khan Academy ( https://pt.khanacademy.org/)
Portal OBMEP ( https://portaldaobmep.impa.br/index.php/modulo/lista?serie=3)
Geogebra https://play.google.com/store/apps/details?id=org.geogebra&hl=pt_BR
Para este plano, foque na etapa AQUECIMENTO
Aquecimento
Sugerimos uma ‘aula invertida’ com o uso da atividade do Aquecimento. Encaminhe aos alunos a versão impressa da atividade juntamente com a resolução (slide 2) e solicite que os alunos explorem o material para produzir um vídeo explicando como é possível resolver a situação considerando um dos critérios de congruência de triângulos. Você pode ainda dividir a turma em grupos para que cada grupo (individualmente) possa explorar um dos critérios de congruência de triângulos, usando as questões da Atividade principal. Encaminhe um áudio ou vídeo via WhatsApp orientando a atividade e mantenha um canal de comunicação. Solicite que os alunos encaminhem os vídeos para sua apreciação. Determine um tempo máximo para o vídeo.
O link da Khan Academy a seguir trata do tema, você pode usá-lo, caso sua turma tenha acesso à internet (https://pt.khanacademy.org/math/geometry/hs-geo-congruence/hs-geo-triangle-congruence/v/congruent-triangles-and-sss)
Atividade principal
A atividade principal pode ser usada juntamente com o Aquecimento para a aula invertida. Se você fizer essa escolha, lembre de encaminhar a questão e a resposta para os alunos analisarem e produzirem o vídeo. Mas você pode optar também em manter a Atividade principal e as atividades complementares como revisão das aprendizagens em outros momentos. Lembre que, independente de sua escolha, as atividades precisam ser retomadas nas discussões.
Discussão das soluções
Analise os vídeos produzidos pelos alunos para dar o feedback à turma. Através de um áudio ou vídeo, aponte dicas e sugestões, evidencie os conceitos destacados na atividade e evidencie os conhecimentos e esforço dos alunos. Disponibilize um vídeo de cada caso de congruência para toda a turma. Se sua turma dispuser de ferramentas e internet, dê preferência por realizar as discussões em tempo real, através de uma das plataformas sugeridas abaixo. Se não tiver, use o WhatsApp que tem um alcance maior. Mas, não esqueça de manter um canal de comunicação para discussão também dessas novas atividades (atividades complementares e Raio X)
Se for possível discutir em tempo real com sua turma, use o Meet, Hangout ou Zoom e considere apenas os itens e os conceitos de maior relevância.
Você pode usar também o Messenger Sala de aluno https://www.messenger.com/groupcall/LINK:4svjhs7dyZw8zoxm/
Sistematização
xxxx
Encerramento
Use nas discussões ou nas orientações iniciais
Raio X
Use o Raio X e as atividades complementares como forma de revisão para consolidação das aprendizagens. Não esqueça de retomar discussões também dessas atividades e focar nos pontos de aprendizagem mais críticos.
Convite às famílias
Questionar: como ampliar ou reduzir um triângulo?
Este plano de aula foi elaborado pelo Time de Autores NOVA ESCOLA
Autora: Renata Akemi Maekawa
Mentor: Fabricio Eduardo Ferreira
Especialista de área: Pricilla Cerqueira
Habilidade da BNCC
(EF08MA12) Demonstrar propriedades de quadriláteros por meio da identificação da congruência de triângulos.
Objetivos específicos
- Comparar triângulos utilizando critérios de congruência de triângulos para determinar medidas de lados e ângulos desconhecidas.
- Utilizar a propriedade em relação à soma dos ângulos internos de um triângulo para obter informações que permitirão verificar congruência entre triângulos.
- Compreender quando não é possível garantir a congruência entre triângulos.
Conceito-chave
Critérios de congruência de triângulos
Recursos necessários
- Fichas impressas.
- Projetor (se possível)














