Atividade raio x
Plano de Aula
Plano de aula: Quadrados e Tangram
Plano 2 de uma sequência de 5 planos. Veja todos os planos sobre Área e Perímetro do quadrado: quem é proporcional?
Por: Elizabeth Bento
Descrição
Este plano de aula foi elaborado pelo Time de Autores NOVA ESCOLA
Autor: Elizabeth Bento
Mentor: Maria Aparecida Nemet Nascimento
Especialista de área: Fernando Barnabé
Habilidade da BNCC
(EF06MA27) Analisar e descrever as mudanças que ocorrem no perímetro e área de um quadrado quando ampliamos ou reduzimos seus lados por um fator k.
Habilidades necessárias
Determinar perímetro e área de um quadrilátero, reconhecer quando há proporcionalidade entre duas grandezas, comparar figuras por meio de semelhanças diretas.
Objetivos específicos
Concluir que apenas lado e perímetro de um quadrado são proporcionais.
Conceito-chave
Área, perímetro, proporcionalidade, Tangram.
Recursos necessários
- Folha milimetrada;
- Lápis de cor;
- Tesoura;
- Régua.
- Jogo de Tangram.
Habilidades BNCC:
Objetivos de aprendizagem
Concluir que apenas lado e perímetro de um quadrado são proporcionais.
Resumo da aula
Objetivo

Tempo sugerido: 2 minutos
Orientação: Compartilhe o objetivo com a classe.
Aquecimento
Construindo quadrados (slides 3 ao 8)
Tempo sugerido: 9 minutos.
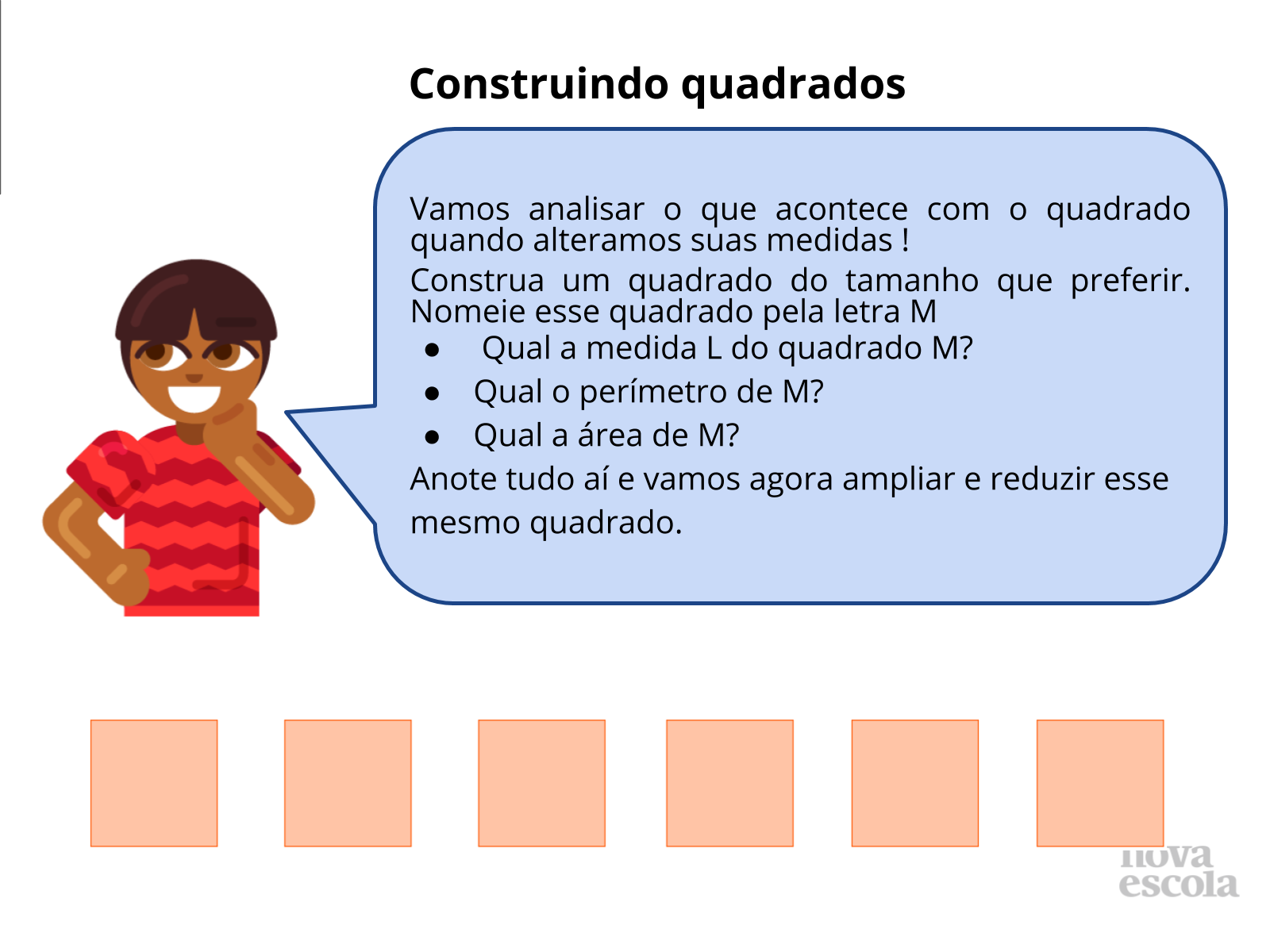
Orientação: Separe a classe em duplas (se necessário trios) e distribua uma folha milimetrada para cada aluno. Orientem a construir um quadrado e que numa mesma folha caiba outros dois, um com a metade do lado e outro com triplo do lado. É comum que alunos chamem qualquer quadrilátero por quadrado, se observar essa ocorrência consulte o Guia de Intervenção aqui.
Propósito: Verificar que não há proporcionalidade entre lado e área, apenas lado e perímetro são proporcionais.
Discuta com a turma:
- O que acontece com a área e perímetro se reduzirmos o lado a quarta parte? Apenas o perímetro fica reduzido a mesma proporção que o lado.
- O que acontece com a área e o perímetro se multiplicarmos seu lado por 4? Apenas o perímetro fica ampliado a mesma proporção que o lado.
- É possível generalizar algum tipo de relação entre lado e perímetro, ou entre lado e área? Lado e perímetro são diretamente proporcionais, enquanto área não. Professor estimule seus alunos a pensarem se há um padrão para ampliar ou reduzir a área de um quadrado, quando multiplicamos seus lados por fator qualquer k.
- Material complementar:
Aquecimento
Construindo quadrados (slides 3 ao 8)
Tempo sugerido: 9 minutos.
Orientação: Separe a classe em duplas (se necessário trios) e distribua uma folha milimetrada para cada aluno. Orientem a construir um quadrado e que numa mesma folha caiba outros dois, um com a metade do lado e outro com triplo do lado. É comum que alunos chamem qualquer quadrilátero por quadrado, se observar essa ocorrência consulte o Guia de Intervenção aqui.
Propósito: Verificar que não há proporcionalidade entre lado e área, apenas lado e perímetro são proporcionais.
Discuta com a turma:
- O que acontece com a área e perímetro se reduzirmos o lado a quarta parte? Apenas o perímetro fica reduzido a mesma proporção que o lado.
- O que acontece com a área e o perimetro se multiplicarmos seu lado por 4? Apenas o perímetro fica ampliado a mesma proporção que o lado.
- É possível generalizar algum tipo de relação entre lado e perímetro, ou entre lado e área? Lado e perímetro são diretamente proporcionais, enquanto área não. Professor estimule seus alunos a pensarem se há um padrão para ampliar ou reduzir a área de um quadrado, quando multiplicamos seus lados por fator qualquer k.
Aquecimento
Construindo quadrados (slides 3 ao 8)
Tempo sugerido: 9 minutos.
Orientação: Separe a classe em duplas (se necessário trios) e distribua uma folha milimetrada para cada aluno. Orientem a construir um quadrado e que numa mesma folha caiba outros dois, um com a metade do lado e outro com triplo do lado. É comum que alunos chamem qualquer quadrilátero por quadrado, se observar essa ocorrência consulte o Guia de Intervenção aqui.
Propósito: Verificar que não há proporcionalidade entre lado e área, apenas lado e perímetro são proporcionais.
Discuta com a turma:
- O que acontece com a área e perímetro se reduzirmos o lado a quarta parte? Apenas o perímetro fica reduzido a mesma proporção que o lado.
- O que acontece com a área e o perimetro se multiplicarmos seu lado por 4? Apenas o perímetro fica ampliado a mesma proporção que o lado.
- É possível generalizar algum tipo de relação entre lado e perímetro, ou entre lado e área? Lado e perímetro são diretamente proporcionais, enquanto área não. Professor estimule seus alunos a pensarem se há um padrão para ampliar ou reduzir a área de um quadrado, quando multiplicamos seus lados por fator qualquer k.
Aquecimento
Construindo quadrados (slides 3 ao 8)
Tempo sugerido: 9 minutos.
Orientação: Separe a classe em duplas (se necessário trios) e distribua uma folha milimetrada para cada aluno. Orientem a construir um quadrado e que numa mesma folha caiba outros dois, um com a metade do lado e outro com triplo do lado. É comum que alunos chamem qualquer quadrilátero por quadrado, se observar essa ocorrência consulte o Guia de Intervenção aqui.
Propósito: Verificar que não há proporcionalidade entre lado e área, apenas lado e perímetro são proporcionais.
Discuta com a turma:
- O que acontece com a área e perímetro se reduzirmos o lado a quarta parte? Apenas o perímetro fica reduzido a mesma proporção que o lado.
- O que acontece com a área e o perimetro se multiplicarmos seu lado por 4? Apenas o perímetro fica ampliado a mesma proporção que o lado.
- É possível generalizar algum tipo de relação entre lado e perímetro, ou entre lado e área? Lado e perímetro são diretamente proporcionais, enquanto área não. Professor estimule seus alunos a pensarem se há um padrão para ampliar ou reduzir a área de um quadrado, quando multiplicamos seus lados por fator qualquer k.
Aquecimento
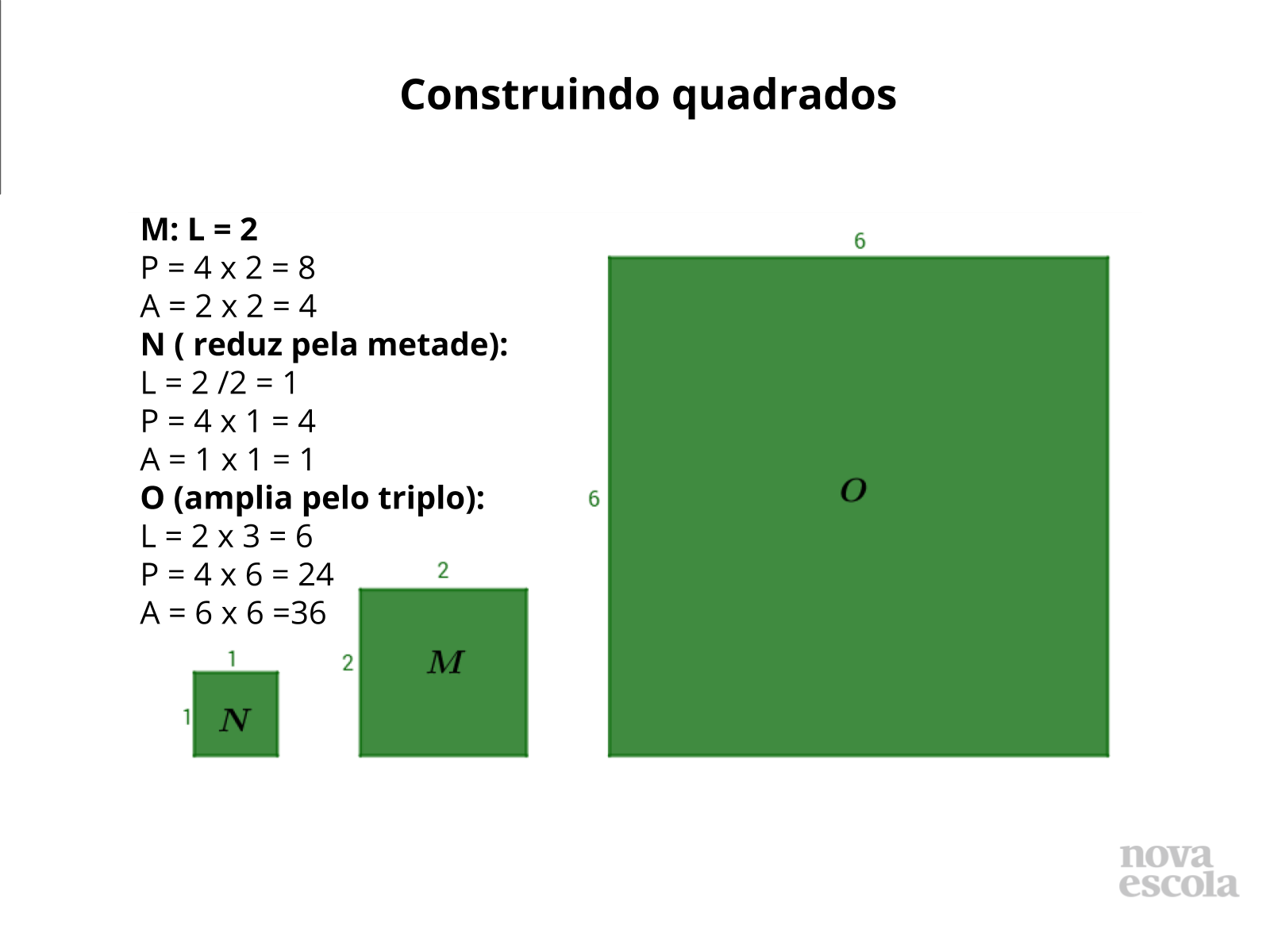
Construindo quadrados (slides 3 ao 8)
Tempo sugerido: 9 minutos.
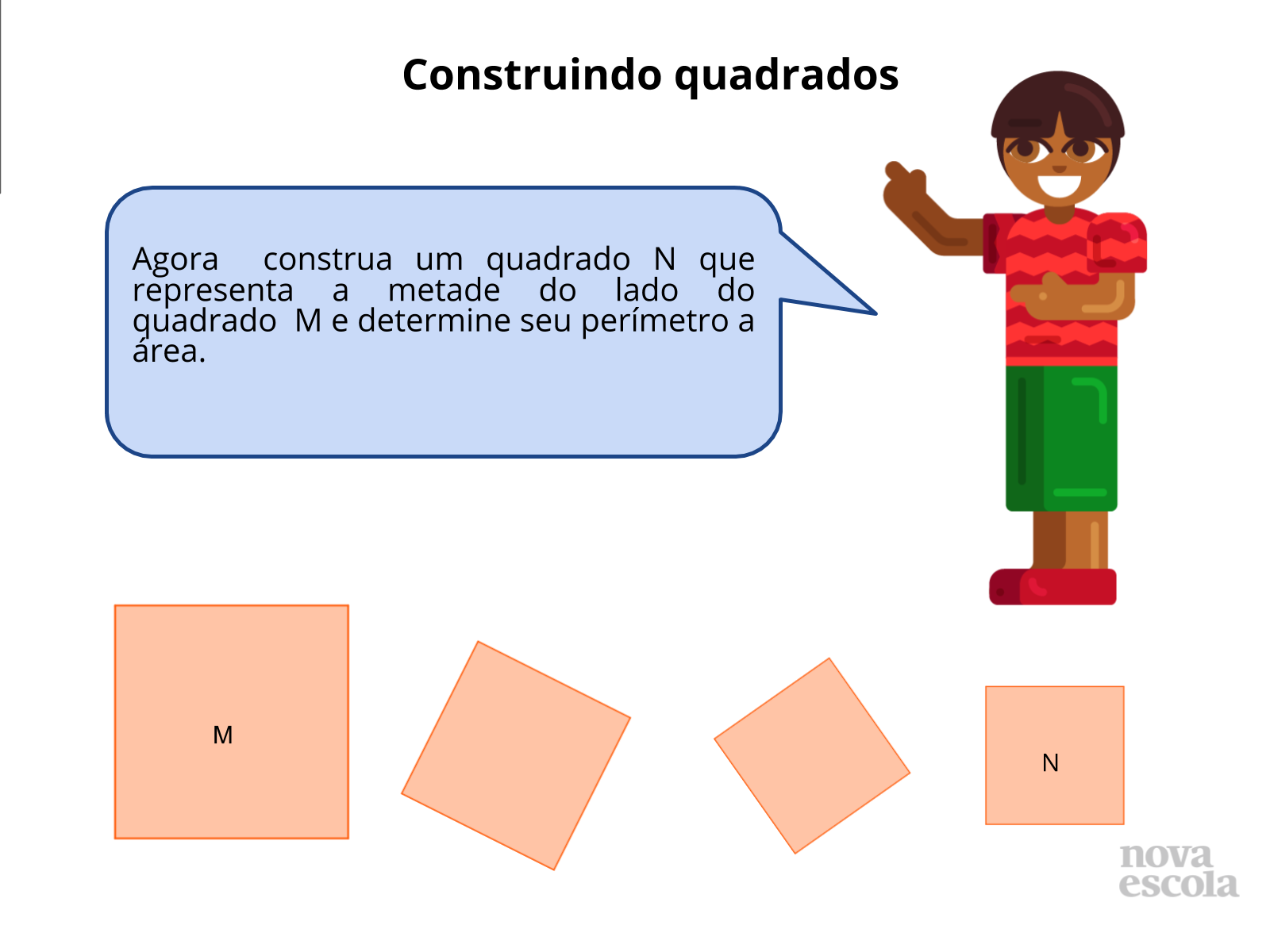
Orientação: Projete as imagens dos quadrados, se possível reproduza outros na lousa com ajuda dos alunos.
Propósito: Verificar que não há proporcionalidade entre lado e área, apenas lado e perímetro são proporcionais.
Discuta com a turma:
- Como você sabe que a figura construída é de fato um quadrado e não um quadrilátero qualquer? Sendo o quadrado construído por uma folha quadriculada ou milimetrada basta observar se os se os lados desse quadrado são paralelos ou que pertencem às mesmas linhas que forma a folha, visto que as linhas da folha são perpendiculares, desta forma o aluno precisa reconhecer que existem os 4 ângulos de 90° e que os lados possuem a mesma medida.
- Podemos dizer que lado e perímetro são proporcionais, porquê? A partir daí é possível que os alunos comecem a generalizar que lado e perímetro de um quadrado são diretamente proporcionais.
Aquecimento
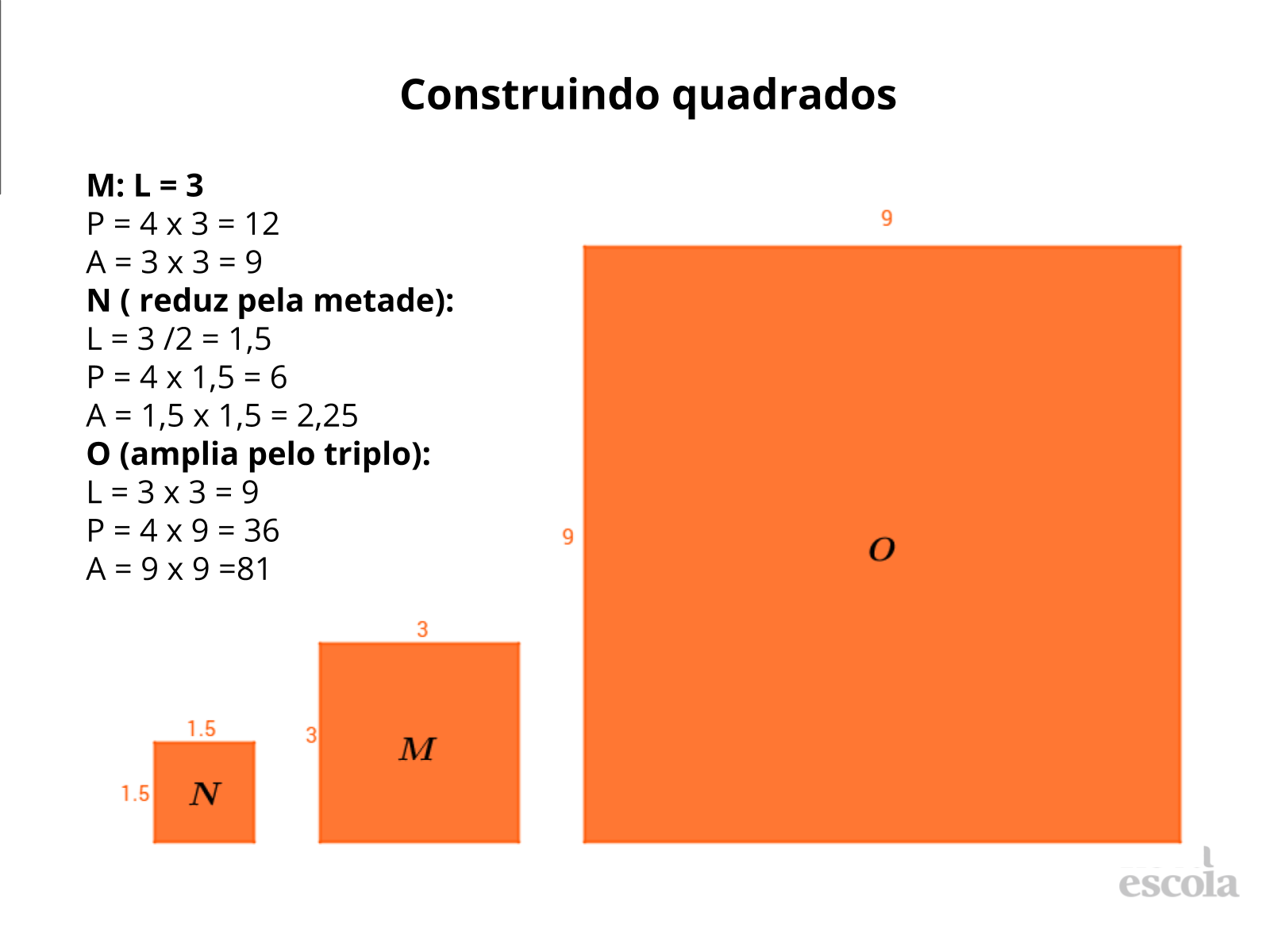
Construindo quadrados (slides 3 ao 8)
Tempo sugerido: 9 minutos.
Orientação: Projete as imagens dos quadrados, se possível reproduza outros na lousa com ajuda dos alunos.
Propósito: Verificar que não há proporcionalidade entre lado e área, apenas lado e perímetro são proporcionais.
Discuta com a turma:
- Como você sabe que a figura construída é de fato um quadrado e não um quadrilátero qualquer? Sendo o quadrado construído por uma folha quadriculada ou milimetrada basta observar se os se os lados desse quadrado são paralelos ou que pertencem às mesmas linhas que forma a folha, visto que as linhas da folha são perpendiculares, desta forma o aluno precisa reconhecer que existem os 4 ângulos de 90° e que os lados possuem a mesma medida.
- Podemos dizer que lado e perímetro são proporcionais, porquê? A partir daí é possível que os alunos comecem a generalizar que lado e perímetro de um quadrado são diretamente proporcionais.
Atividade principal
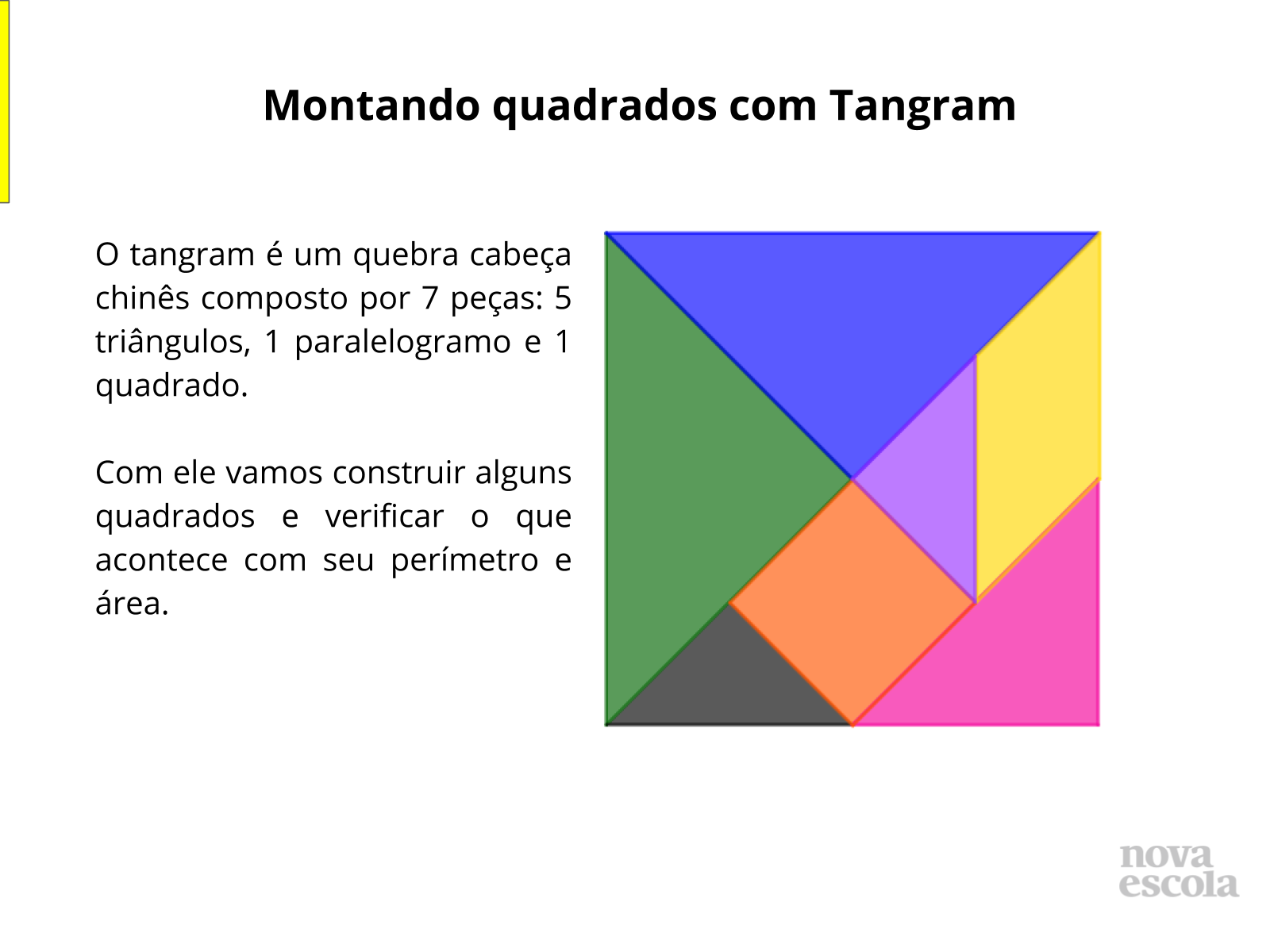
Tempo sugerido: 15 minutos
Orientação: Mantenha as duplas e distribua um kit de tangram, clique aqui para obter o molde, caso não haja possibilidade de imprimir colorido peça para colorir conforme as cores do molde, isso facilitará as soluções.
Propósito: Construir áreas quadradas e investigar o perímetro e área dos quadrados formados por diferentes peças do Tangram.
Discuta com a turma:
- Existe alguma das opções que possuem mais de uma forma de montar o quadrado? As opções com duas, quatro ou sete peças possuem mais de uma forma de montar o quadrado.
- Caso exista, o que aconteceu com o perímetro e área desses quadrados? Permaneceu o mesmo, pois algumas peças possuem a mesma área e partilham lados congruentes.
- O que se observa sobre o perímetro e área dos diferentes quadrados? Nos próximos slides comentamos as ampliações e reduções que acontecem tanto no perímetro como na área dos quadrados formados pelas composições.
- Materiais complementares:
Montando quadrados com Tangram (slides 11 e 12)
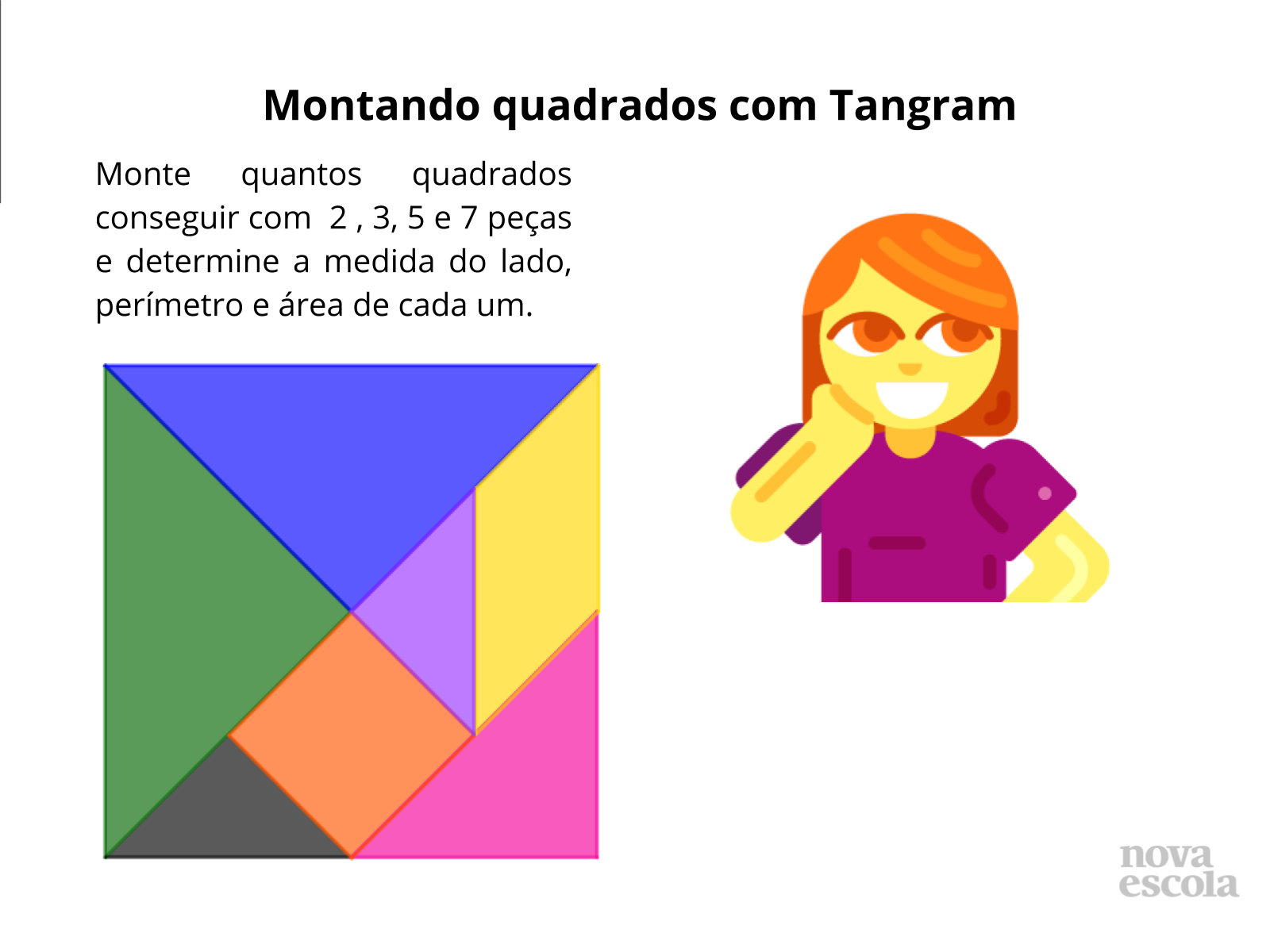
Tempo sugerido: 15 minutos
Orientação: Mantenha as duplas e distribua um kit de tangram, clique aqui para obter o molde, caso não haja possibilidade de imprimir colorido peça para colorir conforme as cores do molde, isso facilitará as soluções.
Propósito: Construir áreas quadradas e investigar o perímetro e área dos quadrados formados por diferentes peças do Tangram.
Discuta com a turma:
- Existe alguma das opções que possuem mais de uma forma de montar o quadrado? As opções com duas, quatro ou sete peças possuem mais de uma forma de montar o quadrado.
- Caso exista, o que aconteceu com o perímetro e área desses quadrados? Permaneceu o mesmo, pois algumas peças possuem a mesma área e partilham lados congruentes.
- O que se observa sobre o perímetro e área dos diferentes quadrados? Nos próximos slides comentamos as ampliações e reduções que acontecem tanto no perímetro como na área dos quadrados formados pelas composições.
Montando quadrados com Tangram - Discussão da Solução (slides 13 ao 18)
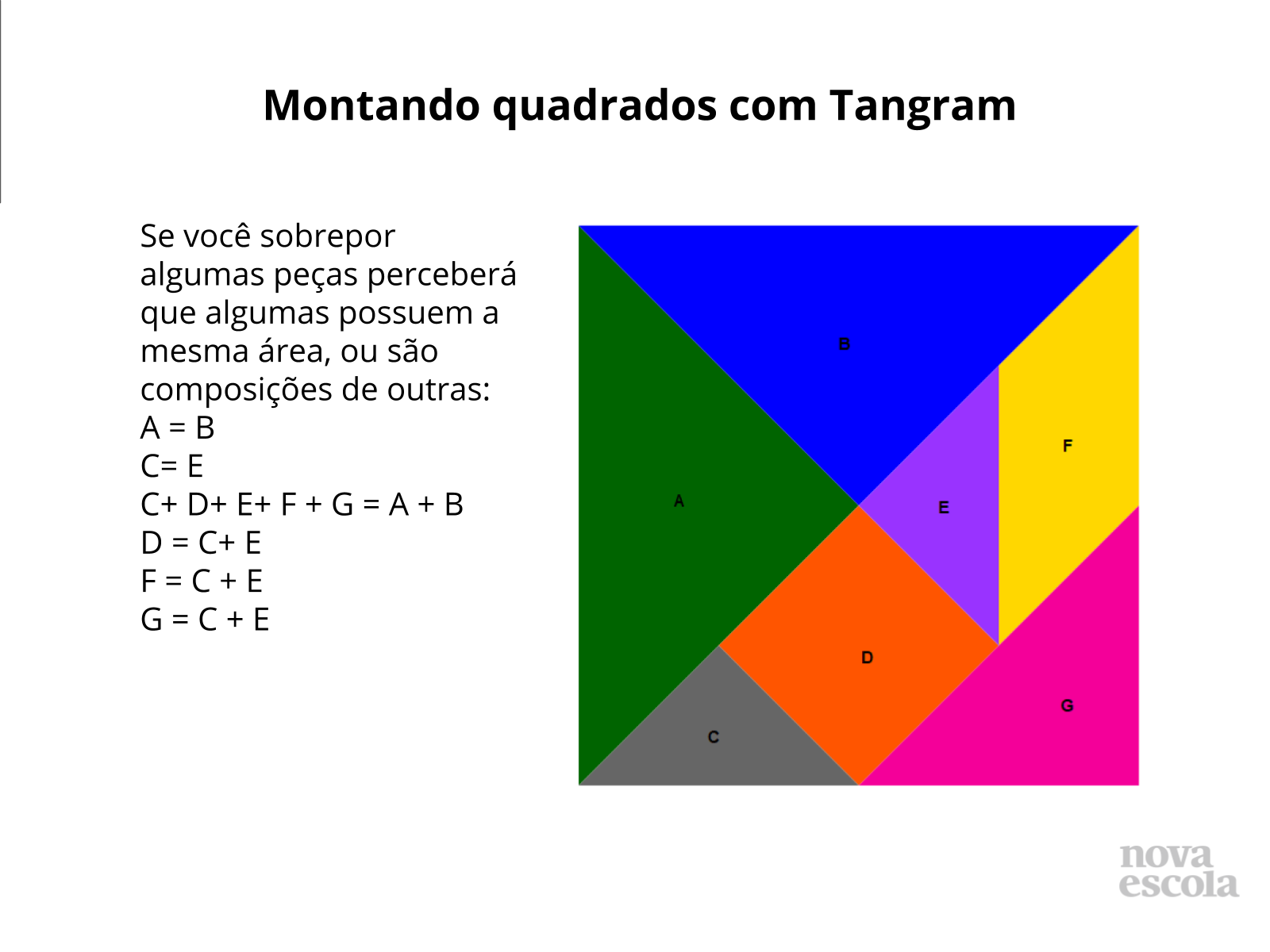
Tempo sugerido: 15 minutos
Orientação: Projete as imagens ou monte os quadrados em EVA ou papel cartão fixando na lousa e identificando- os conforme o slide.
Propósito: Comparar as medidas dos lados e áreas , identificando as proporcionalidades existentes entre lado e perímetro de um quadrado para outro a qual não faz relação com área.
Discuta com a turma: Professor se possível imprima outros moldes do Tangram e outras escalas e peça como dever de casa para que os alunos façam os mesmo procedimentos, determinando lado, perímetro e área e realizando as mesmas comparações, efetuadas em classe.
Montando quadrados com Tangram - Discussão da Solução (slides 13 ao 18)
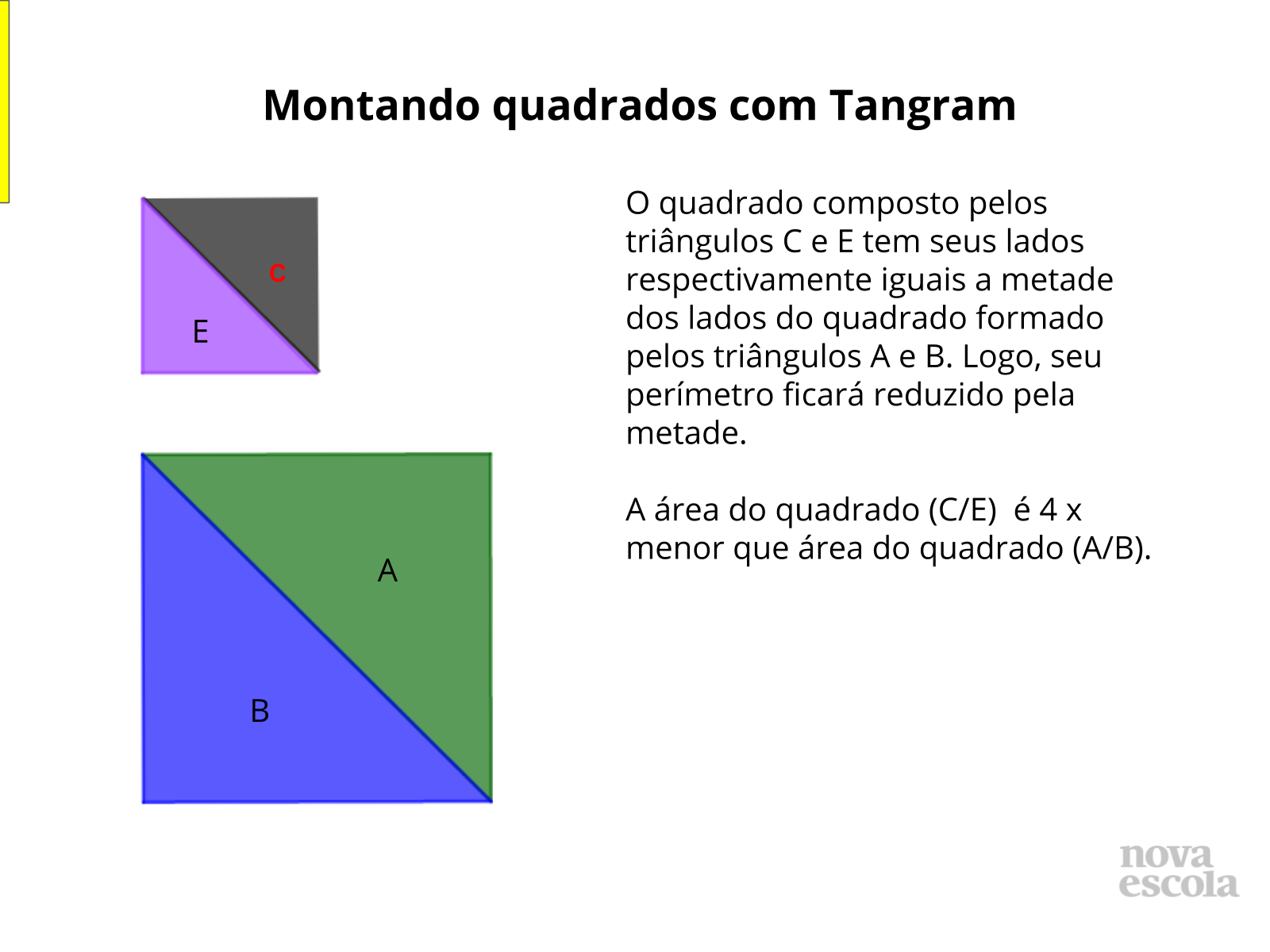
Tempo sugerido: 12 minutos
Orientação: Projete as imagens ou monte os quadrados em EVA ou papel cartão fixando na lousa e identificando- os conforme o slide.
Propósito: Comparar as medidas dos lados e áreas , identificando as proporcionalidades existentes entre lado e perímetro de um quadrado para outro a qual não faz relação com área.
Discuta com a turma: Professor se possível imprima outros moldes do Tangram e outras escalas e peça como dever de casa para que os alunos façam os mesmo procedimentos, determinando lado, perímetro e área e realizando as mesmas comparações, efetuadas em classe.
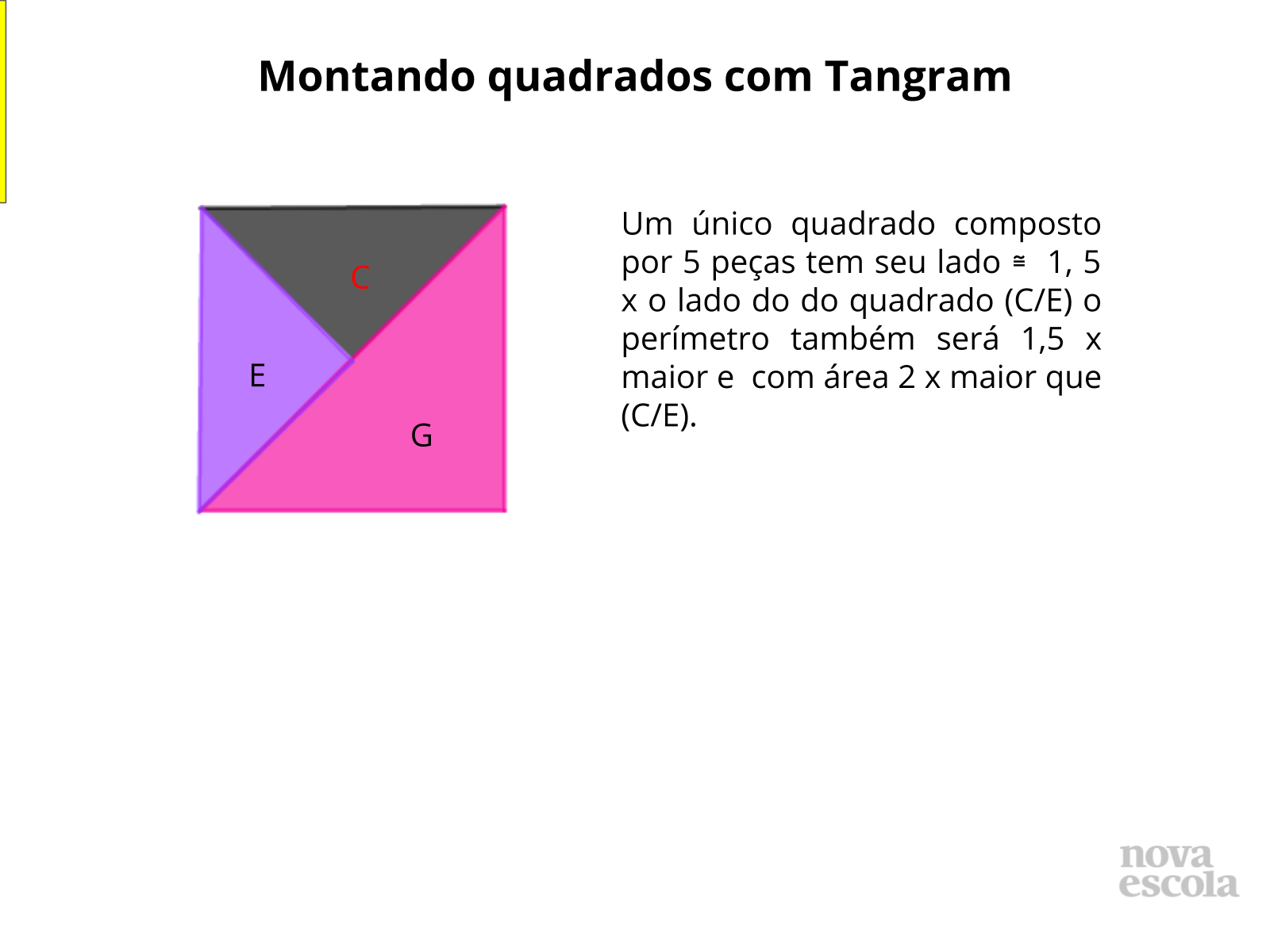
Montando quadrados com Tangram - Discussão da Solução (slides 13 ao 18)
Tempo sugerido: 15 minutos
Orientação: Projete as imagens ou monte os quadrados em EVA ou papel cartão fixando na lousa e identificando- os conforme o slide.
Propósito: Comparar as medidas dos lados e áreas , identificando as proporcionalidades existentes entre lado e perímetro de um quadrado para outro a qual não faz relação com área.
Discuta com a turma: Professor se possível imprima outros moldes do Tangram e outras escalas e peça como dever de casa para que os alunos façam os mesmo procedimentos, determinando lado, perímetro e área e realizando as mesmas comparações, efetuadas em classe.
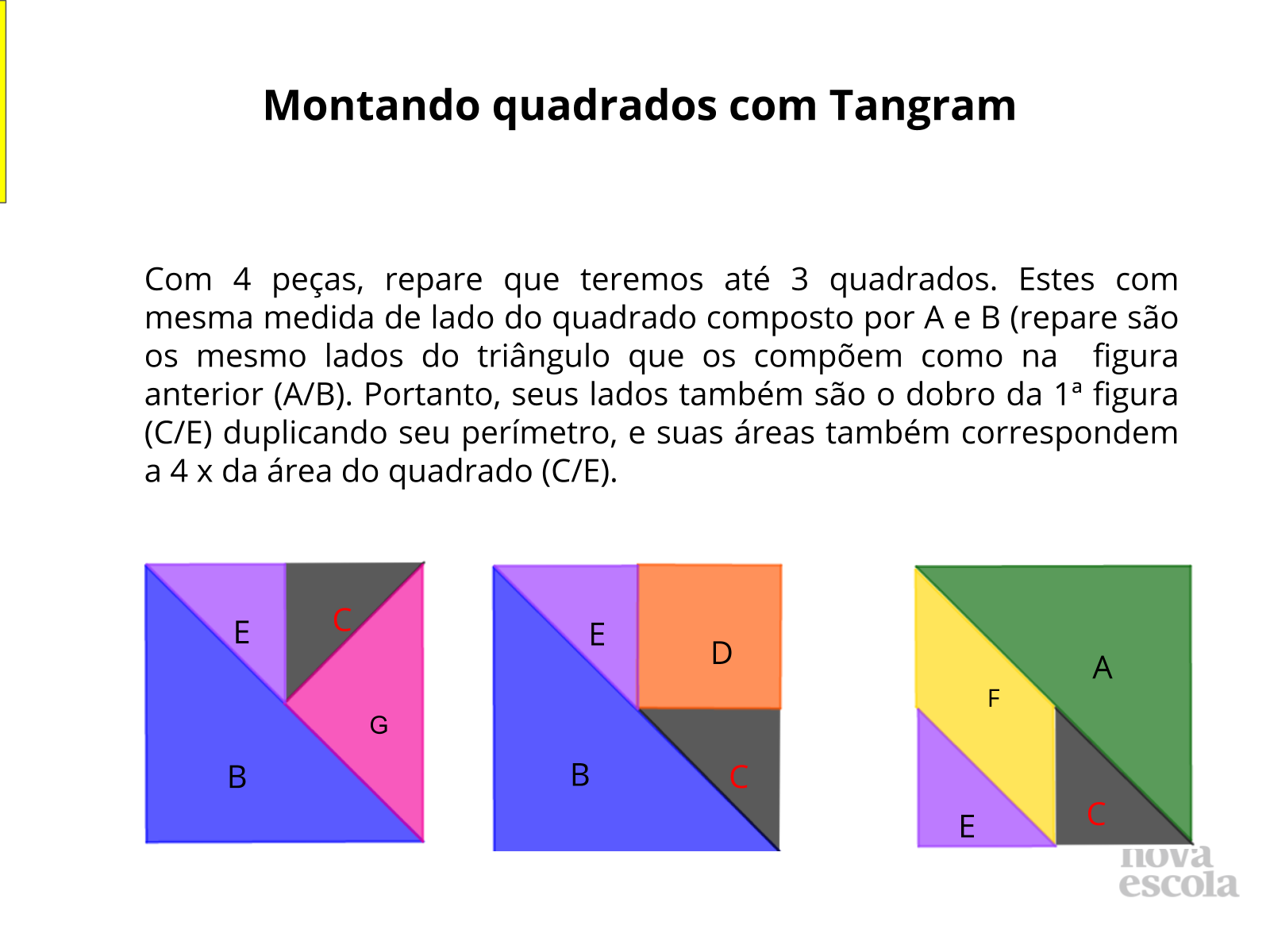
Montando quadrados com Tangram - Discussão da Solução (slides 13 ao 18)
Tempo sugerido: 15 minutos
Orientação: Projete as imagens ou monte os quadrados em EVA ou papel cartão fixando na lousa e identificando- os conforme o slide.
Propósito: Comparar as medidas dos lados e áreas , identificando as proporcionalidades existentes entre lado e perímetro de um quadrado para outro a qual não faz relação com área.
Discuta com a turma: Professor se possível imprima outros moldes do Tangram e outras escalas e peça como dever de casa para que os alunos façam os mesmo procedimentos, determinando lado, perímetro e área e realizando as mesmas comparações, efetuadas em classe.
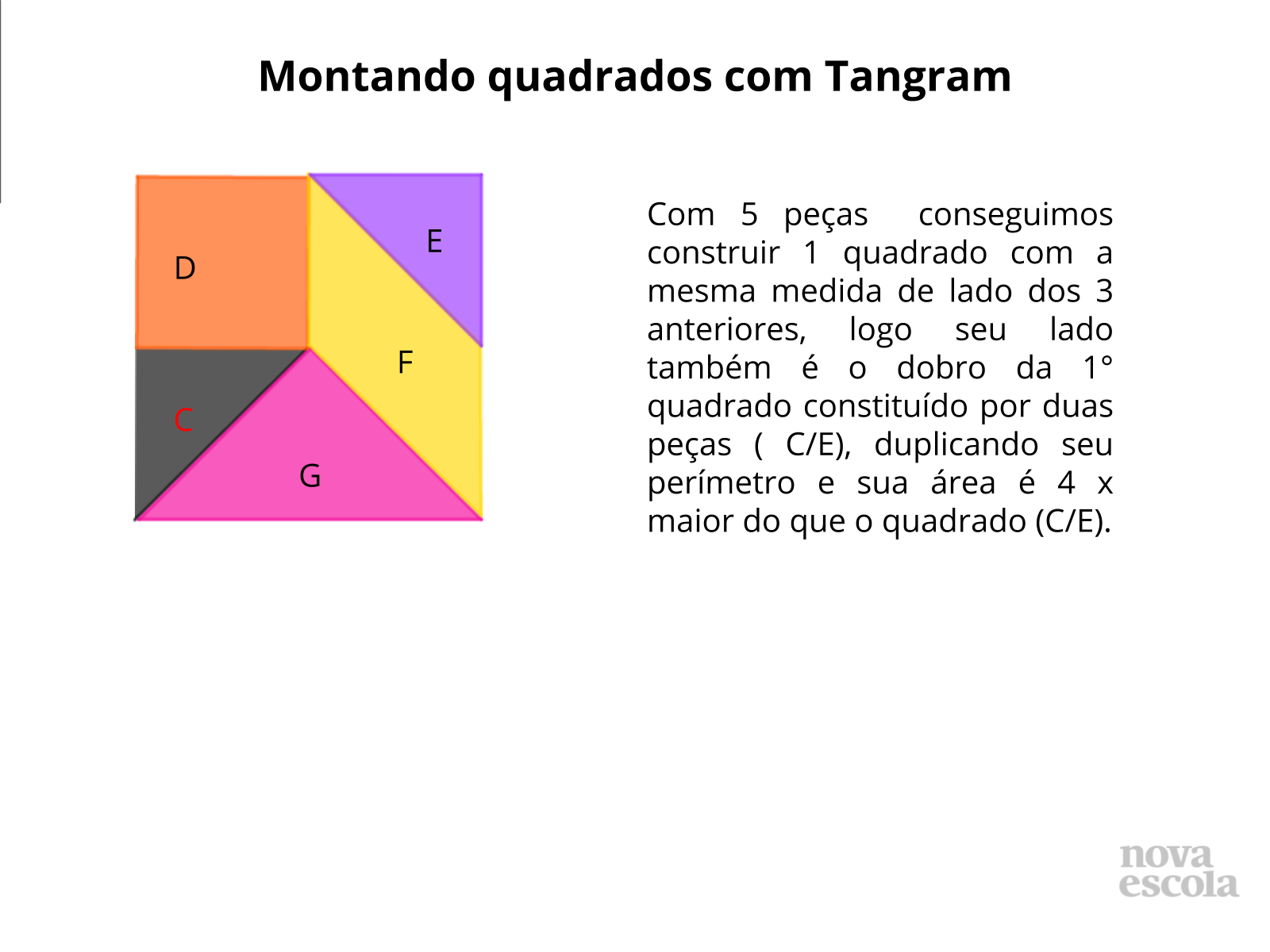
Montando quadrados com Tangram - Discussão da Solução (slides 13 ao 18)
Tempo sugerido: 15 minutos
Orientação: Projete as imagens ou monte os quadrados em EVA ou papel cartão fixando na lousa e identificando- os conforme o slide.
Propósito: Comparar as medidas dos lados e áreas , identificando as proporcionalidades existentes entre lado e perímetro de um quadrado para outro a qual não faz relação com área.
Discuta com a turma: Professor se possível imprima outros moldes do Tangram e outras escalas e peça como dever de casa para que os alunos façam os mesmo procedimentos, determinando lado, perímetro e área e realizando as mesmas comparações, efetuadas em classe.
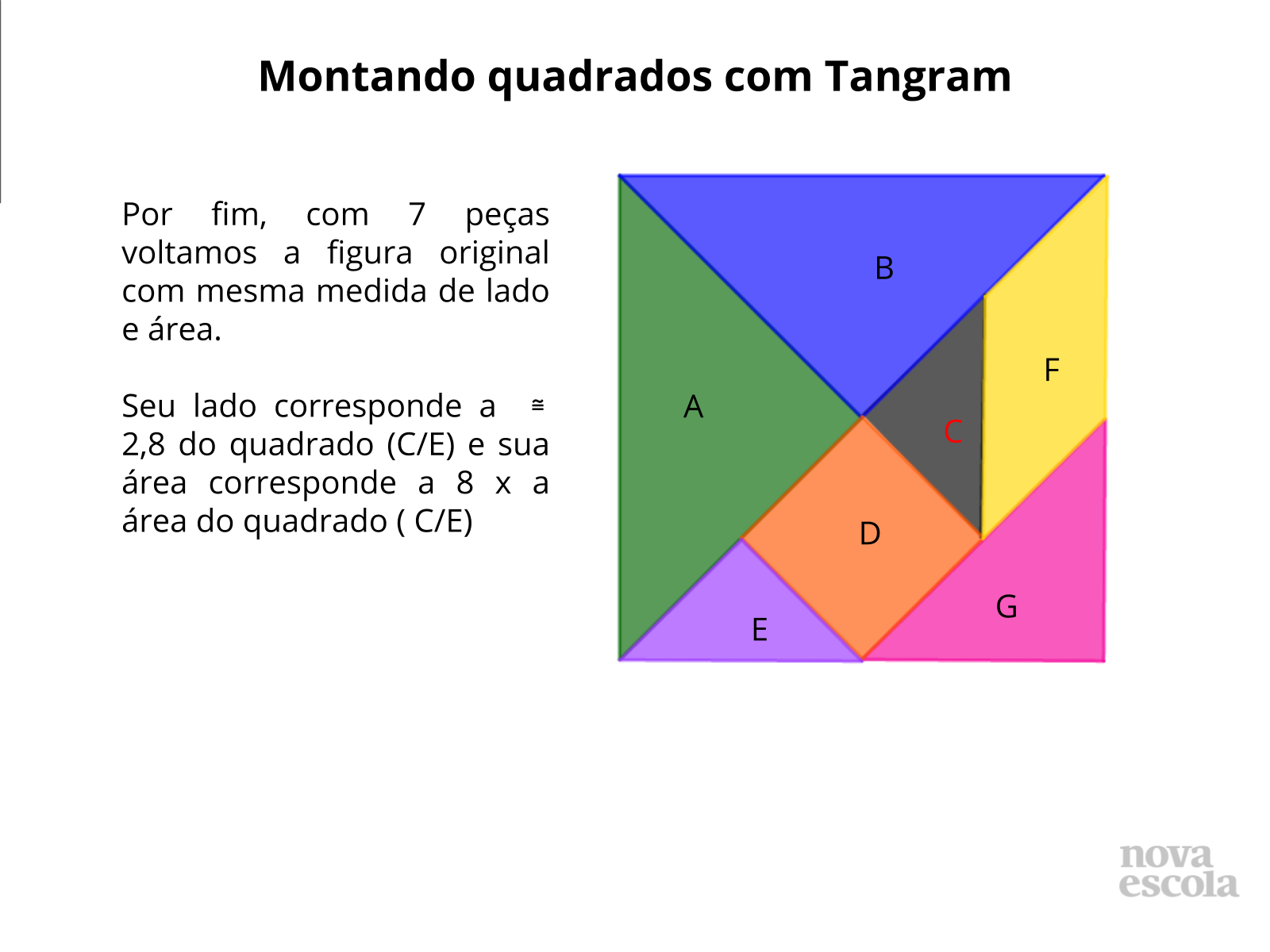
Montando quadrados com Tangram - Discussão da Solução (slides 13 ao 18)
Tempo sugerido: 15 minutos
Orientação: Projete as imagens ou monte os quadrados em EVA ou papel cartão fixando na lousa e identificando- os conforme o slide.
Propósito: Comparar as medidas dos lados e áreas , identificando as proporcionalidades existentes entre lado e perímetro de um quadrado para outro a qual não faz relação com área.
Discuta com a turma: Professor se possível imprima outros moldes do Tangram e outras escalas e peça como dever de casa para que os alunos façam os mesmo procedimentos, determinando lado, perímetro e área e realizando as mesmas comparações, efetuadas em classe.
Encerramento
Tempo sugerido: 2 minutos
Orientação: Leia e comente o conteúdo slide junto com seus alunos.
Raio x
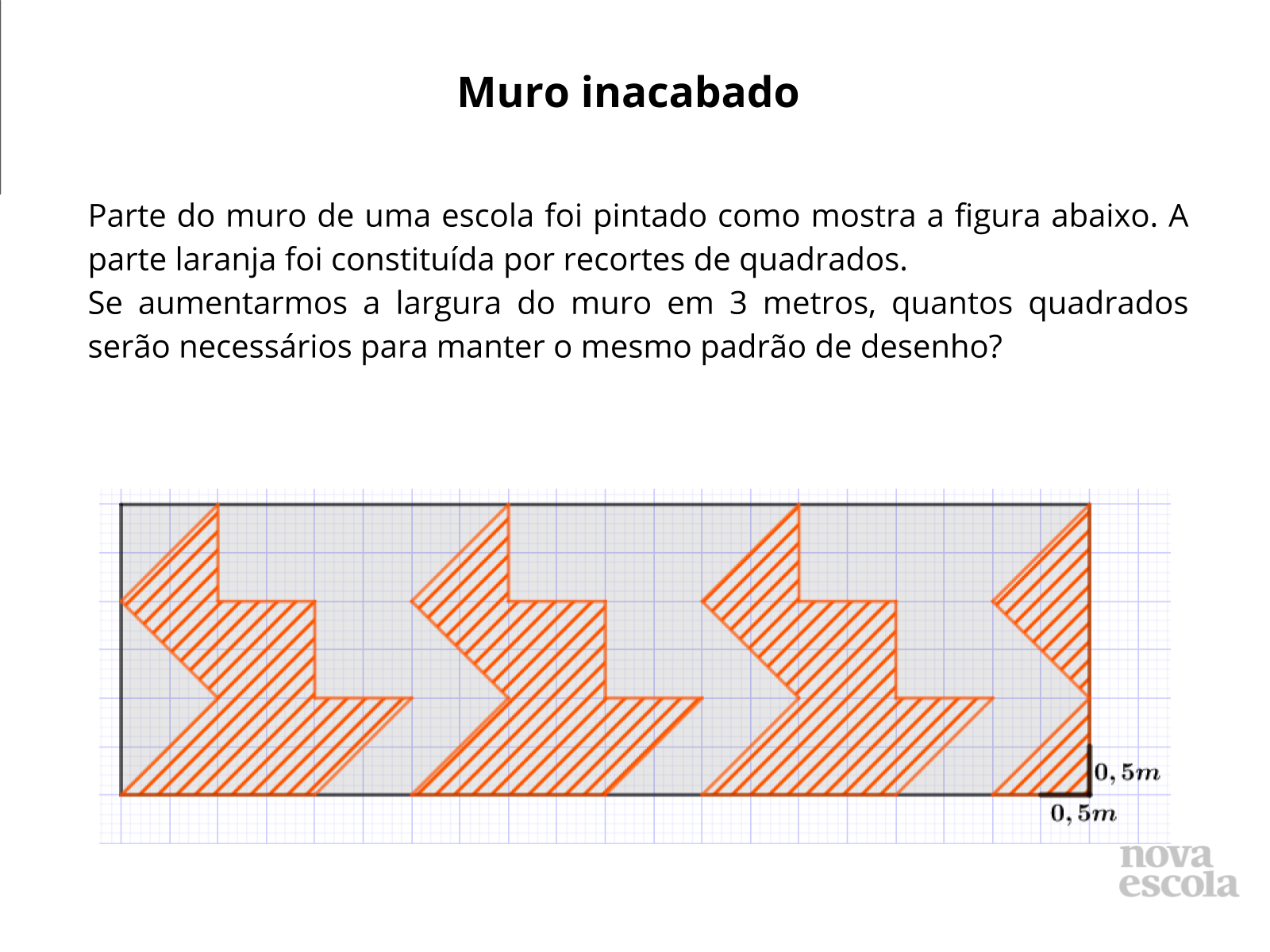
Tempo sugerido: 10 minutos.
Orientação: Para essa atividade é necessário tesoura, régua, cola, um jogo de quadrados laranjas e uma fita retangular que representa o muro da escola (imprima aqui).
Propósito: Investigar área e perímetro de figuras compostas por recortes de quadrados através da manipulação dessas figuras.
Discuta com a turma:
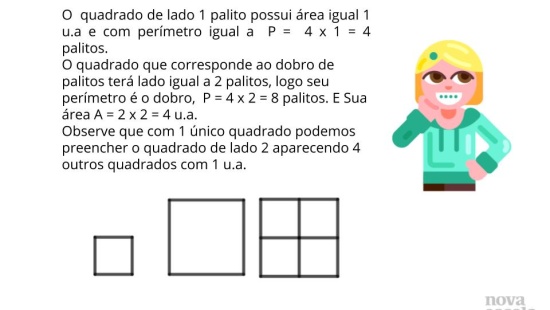
- O que acontece com a área do muro se alterarmos o comprimento e a largura sem modificar o perímetro original? O muro inicial possui 13 x 3 de medida, logo seu perímetro P = 2 x 13 + 2 x 3 = 32 m e sua área A = 3 x 13 = 39 m². Alterando as medidas e conservando o perímetro por exemplo: P = 2 x 14 + 2 x 2 = 32 m e A = 28 m², observa-se que um mesmo perímetro pode cercar áreas distintas, o que dependerá diretamente da medida dos lados.
- O que acontece com a área do muro se mudarmos o formato dele para um quadrado e mantivermos o mesmo perímetro original? O perímetro original corresponde a 32 m, para transformar no perímetro de um quadrado, devemos ter 32 ÷ 4 = 8 e sua área portanto, será A = 8 x 8 = 64 m²
Muro inacabado
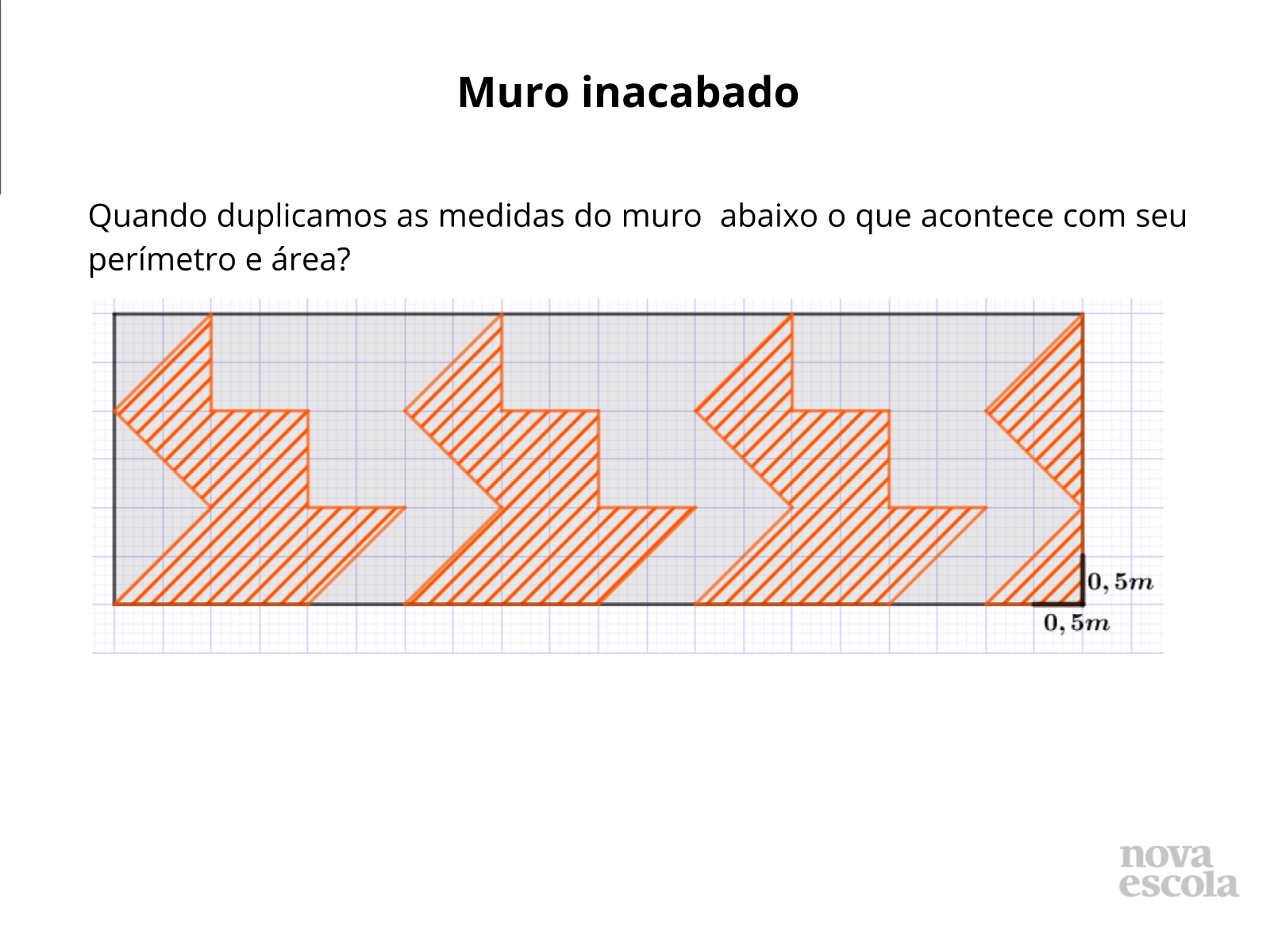
Tempo sugerido: 10 minutos.
Orientação: Para essa atividade é necessário tesoura, régua, cola, um jogo de quadrados laranjas e uma fita retangular que representa o muro da escola (imprima aqui).
Propósito: Investigar área e perímetro de figuras compostas por recortes de quadrados através da manipulação dessas figuras.
Discuta com a turma:
- O que acontece com a área do muro se alterarmos o comprimento e a largura sem modificar o perímetro original? O muro inicial possui 13 x 3 de medida, logo seu perímetro P = 2 x 13 + 2 x 3 = 32 m e sua área A = 3 x 13 = 39 m². Alterando as medidas e conservando o perímetro por exemplo: P = 2 x 14 + 2 x 2 = 32 m e A = 28 m², observa-se que um mesmo perímetro pode cercar áreas distintas, o que dependerá diretamente da medida dos lados.
- O que acontece com a área do muro se mudarmos o formato dele para um quadrado e mantivermos o mesmo perímetro original? O perímetro original corresponde a 32 m, para transformar no perímetro de um quadrado, devemos ter 32 ÷ 4 = 8 e sua área portanto, será A = 8 x 8 = 64 m²
Sugestão de adaptação para ensino remoto
Código do plano
MAT6_22GRM02
Recursos
- Necessários: Caderno, lápis, régua, tesoura, folha ofício
- Opcionais: Zoom, Meet, WhatsApp
Testando área e perímetro: https://www.youtube.com/watch?v=7vyh1i2FNU8
Para este plano foque na etapa Atividade Principal.
Atividade Principal
Compartilhe o slide do “Atividade Principal” (arquivo do Tangram). O objetivo da aula é construir quadrados utilizando as peças do Tangram e verificar o que acontece com a área e o perímetro. Envie com antecedência para os alunos via WhatsApp, Meet ou outro meio de comunicação combinado com eles. Peça que eles imprimam ou reproduzam em uma folha ofício e, em seguida, pintem e recortem. Oriente-os para que eles façam no caderno e fotografem e enviem para você os registros e os cálculos realizados. Eles podem falar entre si em grupos formados por WhatsApp ou, se tiverem pelo Zoom, pode criar salas para que resolvam em grupos a situação. Em seguida, abra o áudio para ouvir as possíveis soluções.
Se sua aula fora assíncrona você pode deixar a atividade impressa na escola ou enviar pelo grupo de WhatsApp e combinar um retorno com eles para uma devolutiva. Nesse retorno, você pode enviar um áudio, registros de outros alunos para que eles comparem com suas estratégias e colem no seu caderno como repertório de soluções.
Discussão das soluções
Avalie as respostas e dúvidas apresentadas pelos alunos para dar um feedback à turma. Se sua aula for síncrona, abra o áudio e ouça as hipóteses ou dúvidas vivenciadas por eles. Certifique os registros enviados pelos alunos, caso contrário, compartilhe as diferentes soluções de construção de quadrados com as peças do Tangram. É importante que eles percebam que algumas vão possuir as mesmas áreas. Faça com duas figuras, por exemplo, dois triângulos, e mostre o cálculo da área. Em seguida, peça que eles, com as peças feitas, procurem construir outros quadrados. Esse é um momento importante da aula: comparar as medidas dos lados e áreas, identificando as proporcionalidades existentes entre lado e perímetro de um quadrado para outro a qual não faz relação com área. Se eles não conseguirem, deixe as peças separadas para que faça a discussão. A comparação entre um quadrado que tenha a mesma área e um que não tenha e outro que não tenha nenhuma relação. Questione: O que podemos concluir em relação à área e perímetro? E a do lado e perímetro? Prepare um áudio com explicação para um fechamento da aula.
Convite às famílias
A participação das famílias no processo de aprendizagem é de grande importância para o aluno. Porém, ressaltamos que os pais não são professores de matemática e muitos estão ocupados nessa fase com outras funções em casa. Peça às famílias, que oportunamente, auxiliem na leitura das comandas e no envio das soluções, conforme os combinados com o professor. É importante que as famílias acompanhem as atividades nos canais de comunicação estabelecidos entre vocês.
Este plano de aula foi elaborado pelo Time de Autores NOVA ESCOLA
Autor: Elizabeth Bento
Mentor: Maria Aparecida Nemet Nascimento
Especialista de área: Fernando Barnabé
Habilidade da BNCC
(EF06MA27) Analisar e descrever as mudanças que ocorrem no perímetro e área de um quadrado quando ampliamos ou reduzimos seus lados por um fator k.
Habilidades necessárias
Determinar perímetro e área de um quadrilátero, reconhecer quando há proporcionalidade entre duas grandezas, comparar figuras por meio de semelhanças diretas.
Objetivos específicos
Concluir que apenas lado e perímetro de um quadrado são proporcionais.
Conceito-chave
Área, perímetro, proporcionalidade, Tangram.
Recursos necessários
- Folha milimetrada;
- Lápis de cor;
- Tesoura;
- Régua.
- Jogo de Tangram.