Atividade Principal
Plano de Aula
Plano de aula: Entendendo e escrevendo uma demonstração matemática
Plano 10 de uma sequência de 10 planos. Veja todos os planos sobre Transformações isométricas e congruência de triângulos
Descrição
Este plano de aula foi elaborado pelo Time de Autores NOVA ESCOLA
Autora: Renata Akemi Maekawa
Mentor: Fabricio Eduardo Ferreira
Especialista de área: Pricilla Cerqueira
Habilidade da BNCC
EF08MA12 - Demonstrar propriedades de quadriláteros por meio da identificação da congruência de triângulos.
EF08MA15 - Reconhecer e construir figuras obtidas por composições de transformações geométricas (translação, reflexão e rotação), com o uso de instrumentos de desenho ou de softwares de geometria dinâmica.
Objetivos específicos
-Retomar as propriedades sobre a soma dos ângulos internos de triângulos e quadriláteros.
-Retomar os critérios de congruência de triângulos.
-Compreender e elaborar demonstrações matemáticas.
Conceito-chave
Demonstrações matemáticas de propriedades geométricas
Recursos necessários
-Fichas impressas.
-Projetor (se possível)
Habilidades BNCC:
Objetivos de aprendizagem
-Retomar as propriedades sobre a soma dos ângulos internos de triângulos e quadriláteros.
-Retomar os critérios de congruência de triângulos.
-Compreender e elaborar demonstrações matemáticas.
Resumo da aula
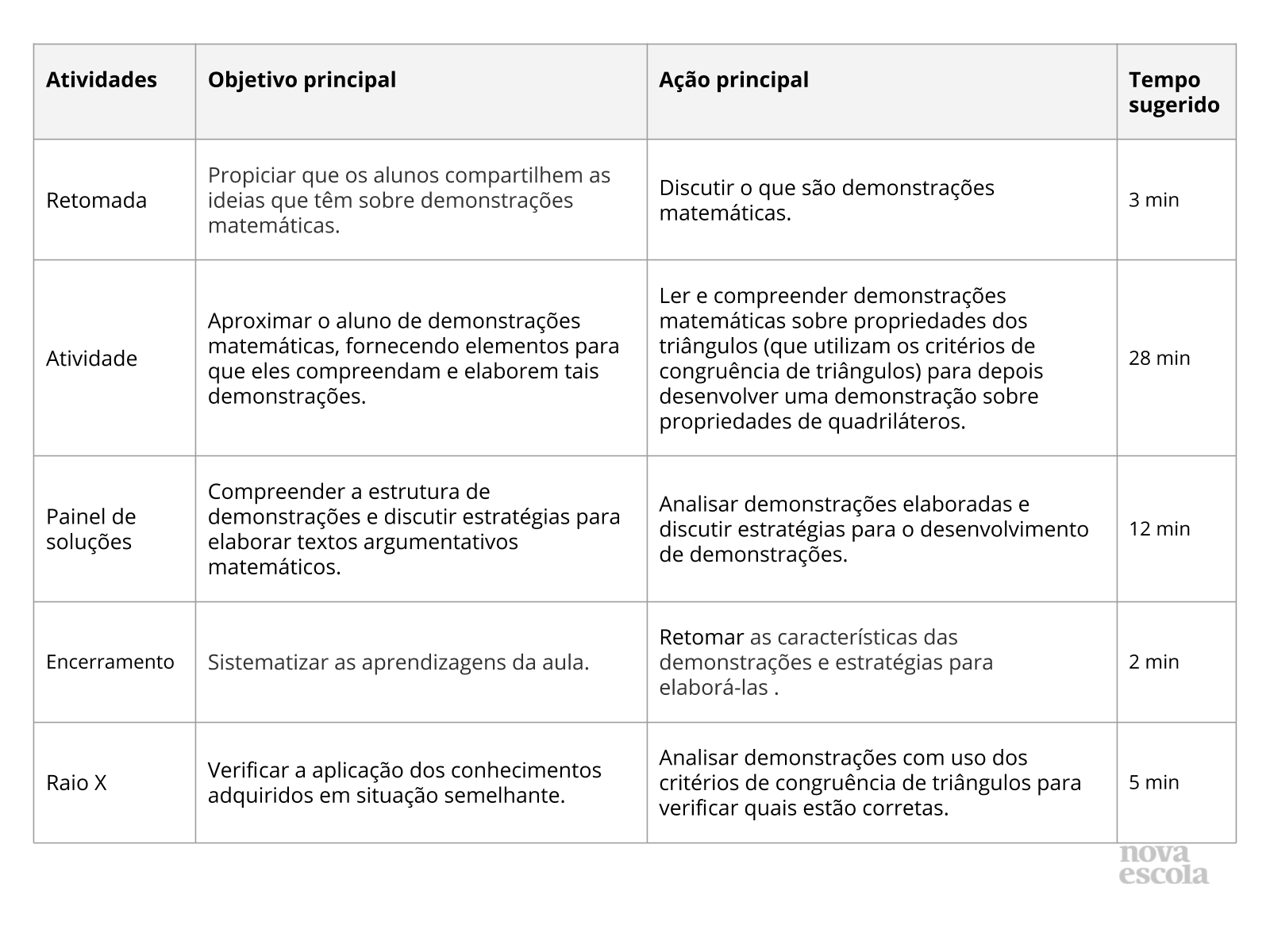
Orientações:Este slide não é um substituto para as anotações para o professor e não deve ser apresentado para os alunos. Trata-se apenas de um resumo da proposta para apoiá-lo na aplicação do plano em sala de aula.
Orientação: Leia atentamente o plano inteiro e as anotações para o professor. Busque antecipar quais questões podem surgir com a sua turma e preveja adequações ao nível em que seus alunos estão.
Compartilhe o objetivo da aula com os alunos antes de aplicar proposta.
Na aba “Sobre o plano”, confira os conhecimentos que sua turma já deve dominar para seguir essa proposta.
Se quiser salvar o plano no seu computador, faça download dos slides na aba “Materiais complementares”. Você também pode imprimi-lo clicando no botão “imprimir”.
Objetivo

Tempo sugerido: 2 minutos.
Orientação: Projete ou leia o objetivo para a turma.
Propósito: Compartilhar o objetivo da aula.
Retomada

Tempo sugerido: 3 minutos.
Orientações: Inicie a aula projetando o questionamento e leia para os alunos (ou apenas leia se o recurso de projeção não estiver disponível). Abra para que os alunos compartilhem o que entendem de uma demonstração matemática. É interessante comentar que as demonstrações matemáticas fazem parte do trabalho dos matemáticos. Nesse momento, é importante que os alunos levantem as características das demonstrações e que compreendam que deve haver presença de argumentos com um encadeamento lógico.
Propósito: Propiciar que os alunos conheçam as características das demonstrações matemáticas.
Discuta com a turma:
- Quais são as características de uma demonstração matemática?
- Qual é a diferença entre enunciar uma propriedade e demonstrar uma propriedade?
Atividade principal

Tempo sugerido: 1 minuto
Orientação: Leia o texto para os alunos ou projete-o. Retome o valor da soma dos ângulos internos dos triângulos e destaque a eles trabalharão com a demonstração desta propriedade, que é diferente de somente afirmar que esta soma é sempre igual a 180º.
Propósito: antecipar qual será o foco da atividade e destacar a diferença entre enunciar uma propriedade e demonstrar uma propriedade.
Materiais complementares para impressão:
Atividade Principal
Atividade principal

Tempo sugerido: 8 minutos (slides 5 a 7).
Orientação: Projete a atividade que está nos slides 5 a 7 ou imprima e entregue uma cópia para cada aluno. Organize os alunos em duplas heterogêneas e solicite que eles leiam a demonstração individualmente e depois leiam novamente com a dupla, verificando se compreenderam todas as etapas. Abra para que os alunos compartilhem as dúvidas que não conseguirem resolver nas duplas e para que a classe destaque as características da demonstração fornecida.
Propósito: propiciar que os alunos tenham contato com uma demonstração matemática e analisem suas características.
Discuta com a turma:
- Podemos afirmar que foram apresentados argumentos matemáticos nessa demonstração?
- As imagens auxiliaram na compreensão?
- Que parte do texto podemos associar à conclusão da demonstração?
Materiais complementares para impressão:
Atividade Principal
Resolução da Atividade Principal
Atividade principal
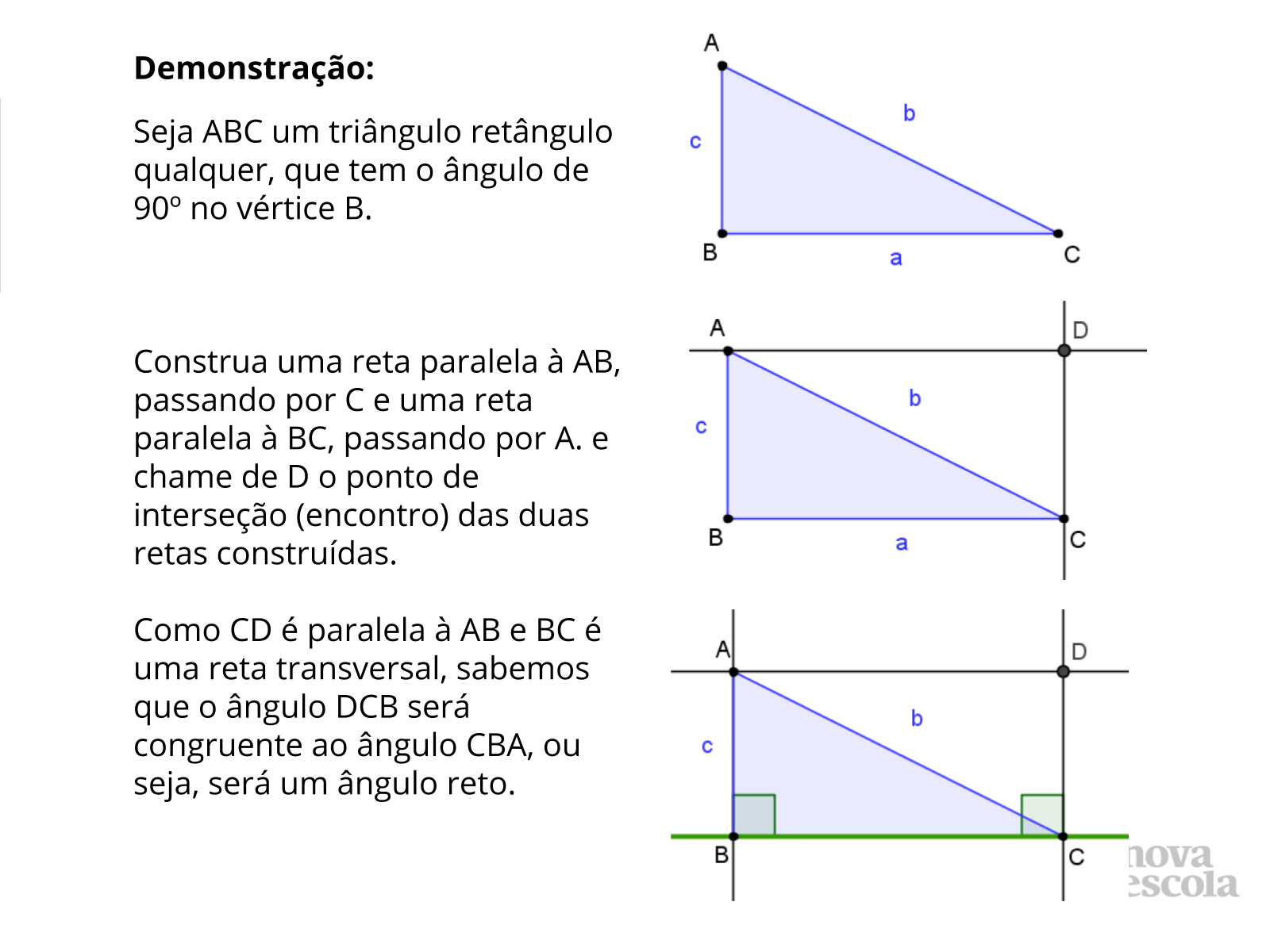
Tempo sugerido: 8 minutos (slides 5 a 7).
Orientação: Projete a atividade que está nos slides 5 a 7 ou imprima e entregue uma cópia para cada aluno. Organize os alunos em duplas heterogêneas e solicite que eles leiam a demonstração individualmente e depois leiam novamente com a dupla, verificando se compreenderam todas as etapas. Abra para que os alunos compartilhem as dúvidas que não conseguirem resolver nas duplas e para que a classe destaque as características da demonstração fornecida.
Propósito: propiciar que os alunos tenham contato com uma demonstração matemática e analisem suas características.
Discuta com a turma:
- Podemos afirmar que foram apresentados argumentos matemáticos nessa demonstração?
- As imagens auxiliaram na compreensão?
- Que parte do texto podemos associar à conclusão da demonstração?
Atividade principal
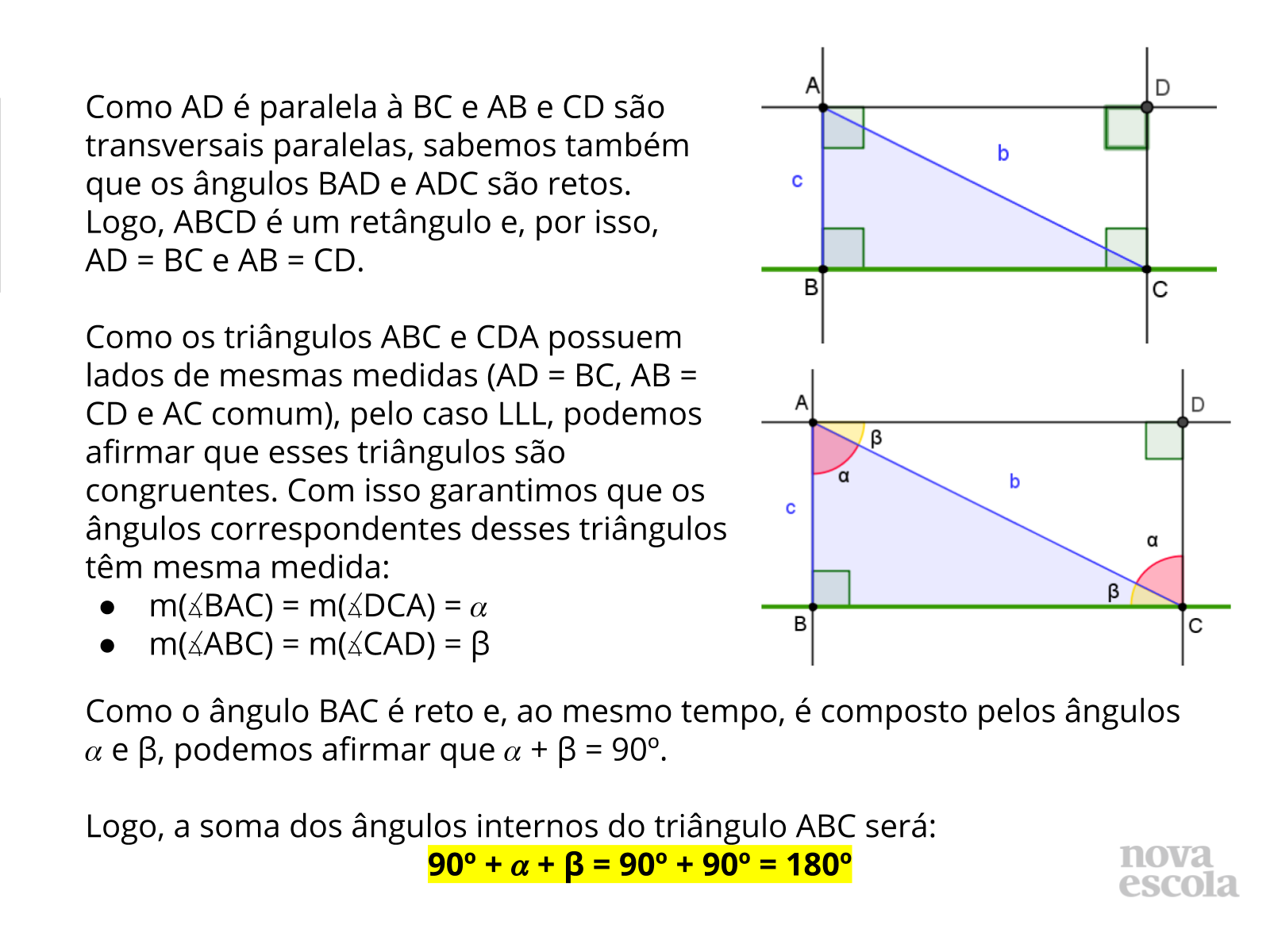
Tempo sugerido: 8 minutos (slides 5 a 7).
Orientação: Projete a atividade que está nos slides 5 a 7 ou imprima e entregue uma cópia para cada aluno. Organize os alunos em duplas heterogêneas e solicite que eles leiam a demonstração individualmente e depois leiam novamente com a dupla, verificando se compreenderam todas as etapas. Abra para que os alunos compartilhem as dúvidas que não conseguirem resolver nas duplas e para que a classe destaque as características da demonstração fornecida.
Propósito: propiciar que os alunos tenham contato com uma demonstração matemática e analisem suas características.
Discuta com a turma:
- Podemos afirmar que foram apresentados argumentos matemáticos nessa demonstração?
- As imagens auxiliaram na compreensão?
- Que parte do texto podemos associar à conclusão da demonstração?
Atividade principal

Tempo sugerido: 20 minutos (slides 8 a 11).
Orientação: Projete as atividades que estão nos slides 8 a 11 ou dê continuidade à atividade impressa. Organize os alunos quartetos, juntando duas duplas que trabalharam juntas no momento anterior. Solicite que eles resolvam a atividade 2 individualmente e depois compartilhem a enumeração e a associação de imagens elaborada no grupo e discutam, caso haja diferença entre as resposta. Oriente que leiam a demonstração utilizando a enumeração elaborada para verificar se o texto gerado ficou coerente. Você pode optar por entregar as figuras para os alunos recortarem e colarem nos espaços indicados. O arquivo para impressão estará disponível nos materiais complementares.
Depois, peça para que eles resolvam a atividade 3 nas duplas e que, em seguida, leiam as demonstrações elaboradas para a outra dupla do quarteto para discutirem se estão completas e corretas. A partir das demonstrações elaboradas pelas duplas, o quarteto deve redigir uma demonstração “oficial” do grupo que será utilizada para a discussão coletiva que ocorrerá em seguida.
Circule pela sala para observar como os alunos estão resolvendo o problema, sem informar os grupos se a resposta obtida por eles está correta ou não.
Propósito: propiciar que os alunos elaborem demonstração matemática sobre propriedades de triângulos e quadriláteros.
Materiais complementares para impressão:
Atividade principal
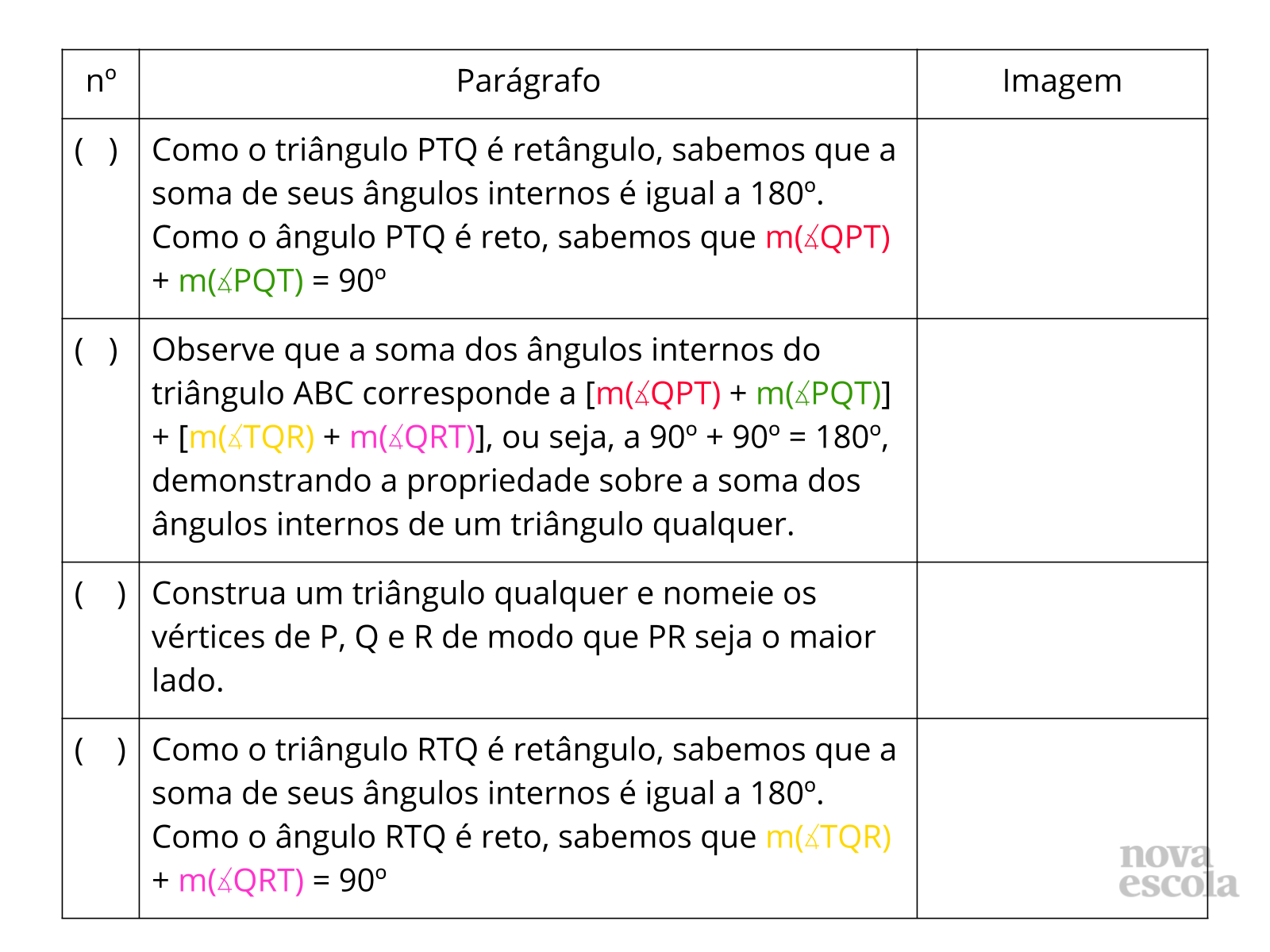
Tempo sugerido: 20 minutos (slides 8 a 11).
Orientação: Projete as atividades que estão nos slides 8 a 11 ou dê continuidade à atividade impressa. Organize os alunos quartetos, juntando duas duplas que trabalharam juntas no momento anterior. Solicite que eles resolvam a atividade 2 individualmente e depois compartilhem a enumeração e a associação de imagens elaborada no grupo e discutam, caso haja diferença entre as resposta. Oriente que leiam a demonstração utilizando a enumeração elaborada para verificar se o texto gerado ficou coerente. Você pode optar por entregar as figuras para os alunos recortarem e colarem nos espaços indicados. O arquivo para impressão estará disponível nos materiais complementares.
Depois, peça para que eles resolvam a atividade 3 nas duplas e que, em seguida, leiam as demonstrações elaboradas para a outra dupla do quarteto para discutirem se estão completas e corretas. A partir das demonstrações elaboradas pelas duplas, o quarteto deve redigir uma demonstração “oficial” do grupo que será utilizada para a discussão coletiva que ocorrerá em seguida.
Circule pela sala para observar como os alunos estão resolvendo o problema, sem informar os grupos se a resposta obtida por eles está correta ou não.
Propósito: propiciar que os alunos elaborem demonstração matemática sobre propriedades de triângulos e quadriláteros.
Materiais complementares para impressão:
Resolução da Atividade Principal
Atividade principal
Tempo sugerido: 20 minutos (slides 8 a 11).
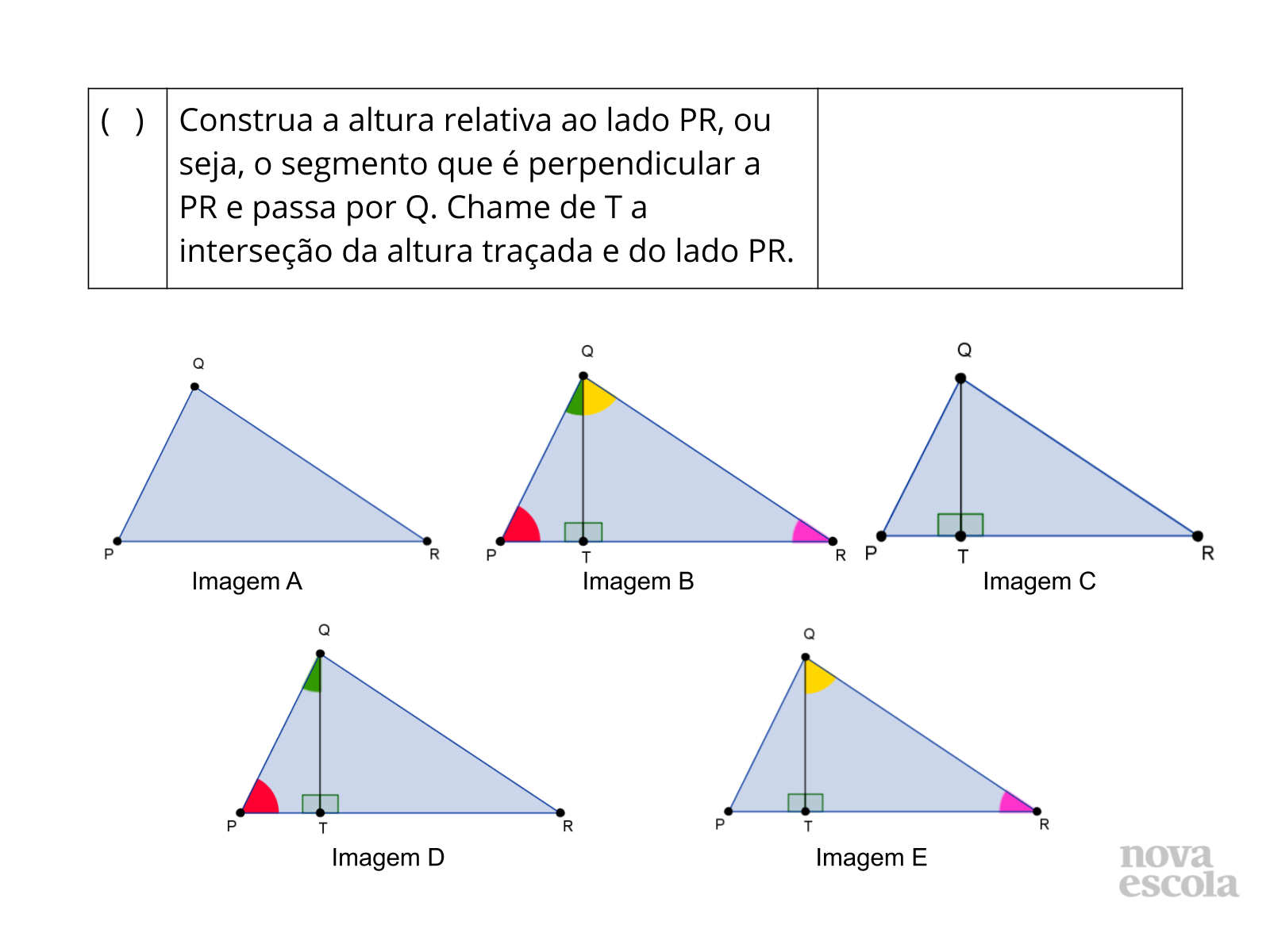
Orientação: Projete as atividades que estão nos slides 8 a 11 ou dê continuidade à atividade impressa. Organize os alunos quartetos, juntando duas duplas que trabalharam juntas no momento anterior. Solicite que eles resolvam a atividade 2 individualmente e depois compartilhem a enumeração e a associação de imagens elaborada no grupo e discutam, caso haja diferença entre as resposta. Oriente que leiam a demonstração utilizando a enumeração elaborada para verificar se o texto gerado ficou coerente. Você pode optar por entregar as figuras para os alunos recortarem e colarem nos espaços indicados. O arquivo para impressão estará disponível nos materiais complementares.
Depois, peça para que eles resolvam a atividade 3 nas duplas e que, em seguida, leiam as demonstrações elaboradas para a outra dupla do quarteto para discutirem se estão completas e corretas. A partir das demonstrações elaboradas pelas duplas, o quarteto deve redigir uma demonstração “oficial” do grupo que será utilizada para a discussão coletiva que ocorrerá em seguida.
Circule pela sala para observar como os alunos estão resolvendo o problema, sem informar os grupos se a resposta obtida por eles está correta ou não.
Propósito: propiciar que os alunos elaborem demonstração matemática sobre propriedades de triângulos e quadriláteros.
Materiais complementares para impressão:
Resolução da Atividade Principal
Atividade principal
Tempo sugerido: 20 minutos (slides 8 a 11).
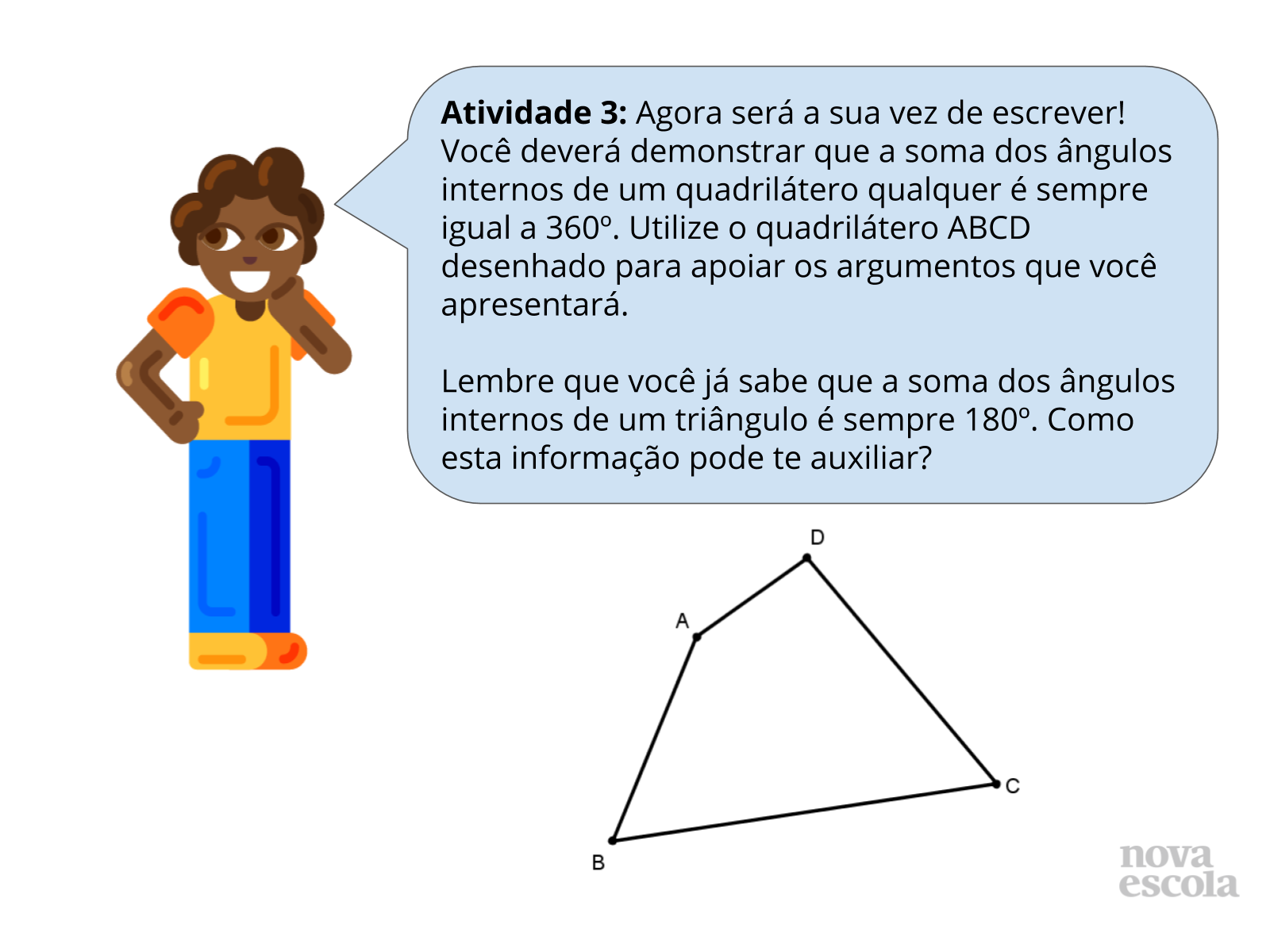
Orientação: Projete as atividades que estão nos slides 8 a 11 ou dê continuidade à atividade impressa. Organize os alunos quartetos, juntando duas duplas que trabalharam juntas no momento anterior. Solicite que eles resolvam a atividade 2 individualmente e depois compartilhem a enumeração e a associação de imagens elaborada no grupo e discutam, caso haja diferença entre as resposta. Oriente que leiam a demonstração utilizando a enumeração elaborada para verificar se o texto gerado ficou coerente. Você pode optar por entregar as figuras para os alunos recortarem e colarem nos espaços indicados. O arquivo para impressão estará disponível nos materiais complementares.
Depois, peça para que eles resolvam a atividade 3 nas duplas e que, em seguida, leiam as demonstrações elaboradas para a outra dupla do quarteto para discutirem se estão completas e corretas. A partir das demonstrações elaboradas pelas duplas, o quarteto deve redigir uma demonstração “oficial” do grupo que será utilizada para a discussão coletiva que ocorrerá em seguida.
Circule pela sala para observar como os alunos estão resolvendo o problema, sem informar os grupos se a resposta obtida por eles está correta ou não.
Propósito: propiciar que os alunos elaborem demonstração matemática sobre propriedades de triângulos e quadriláteros.
Materiais complementares para impressão:
Resolução da Atividade Principal
Painel de soluções

Tempo sugerido: 12 minutos (slides 12 a 15).
Orientações: Escolha um grupo para compartilhar a numeração escolhida para os parágrafos da demonstração da atividade 2. Abra para que os alunos digam se concordam ou não e que compartilhem outras possibilidades de numeração, se tiverem elaborado. Nesta discussão, é importante discutir a possibilidade de inverter a numeração dos parágrafos que destacam os ângulos internos dos triângulos PTQ e RTQ (veja a resolução da atividade para maiores detalhes). Discuta com a classe as estratégias que podem ser utilizadas para resolver problemas desse tipo (de decidir a ordem de parágrafos de uma demonstração). Depois, faça uma leitura coletiva da demonstração utilizando o slide 13. Esta leitura é interessante para aproximar os alunos da estrutura da demonstração e também para que eles compreendam a propriedade dos triângulos sobre a soma dos ângulos internos de maneira mais profunda.
Em seguida, peça para que os alunos leiam as demonstrações “oficiais” do grupo elaboradas na atividade 3 e que reproduzam na lousa as imagens que usaram para apoiar a demonstração. É importante que as diferentes respostas apareçam nesse momento e, por isso, a observação feita das resoluções dos alunos no momento anterior é muito importante para decidir quais grupos chamar para falar. Discuta com a classe se as demonstrações elaboradas estão corretas e completas, se são equivalentes e se estão escritas de um modo que facilita que o leitor as compreenda.
Por fim, se julgar necessário, exiba a demonstração do slide 15 ou escreva-a na lousa para concluir a discussão das soluções.
Propósito: propiciar que os alunos compreendam a estrutura das demonstrações, retomem propriedades de triângulos e quadriláteros e elaborem demonstrações próprias.
Discuta com a turma:
- Que estratégias podemos usar para identificar qual a ordem correta dos parágrafos da demonstração? As imagens podem ajudar? E os termos que aparecem nos parágrafos?
- A demonstração gerada na atividade 2 mostra por que a soma dos ângulos de um triângulo qualquer é sempre 180º? Elaborar esta demonstração é o mesmo que enunciar a propriedade?
- Que estratégias podemos usar para elaborar uma demonstração? Como podemos iniciá-la? E como deve ser a sua finalização?
- Como as imagens podem ajudar a deixar uma demonstração geométrica mais clara?
Painel de soluções
Tempo sugerido: 12 minutos (slides 12 a 15).
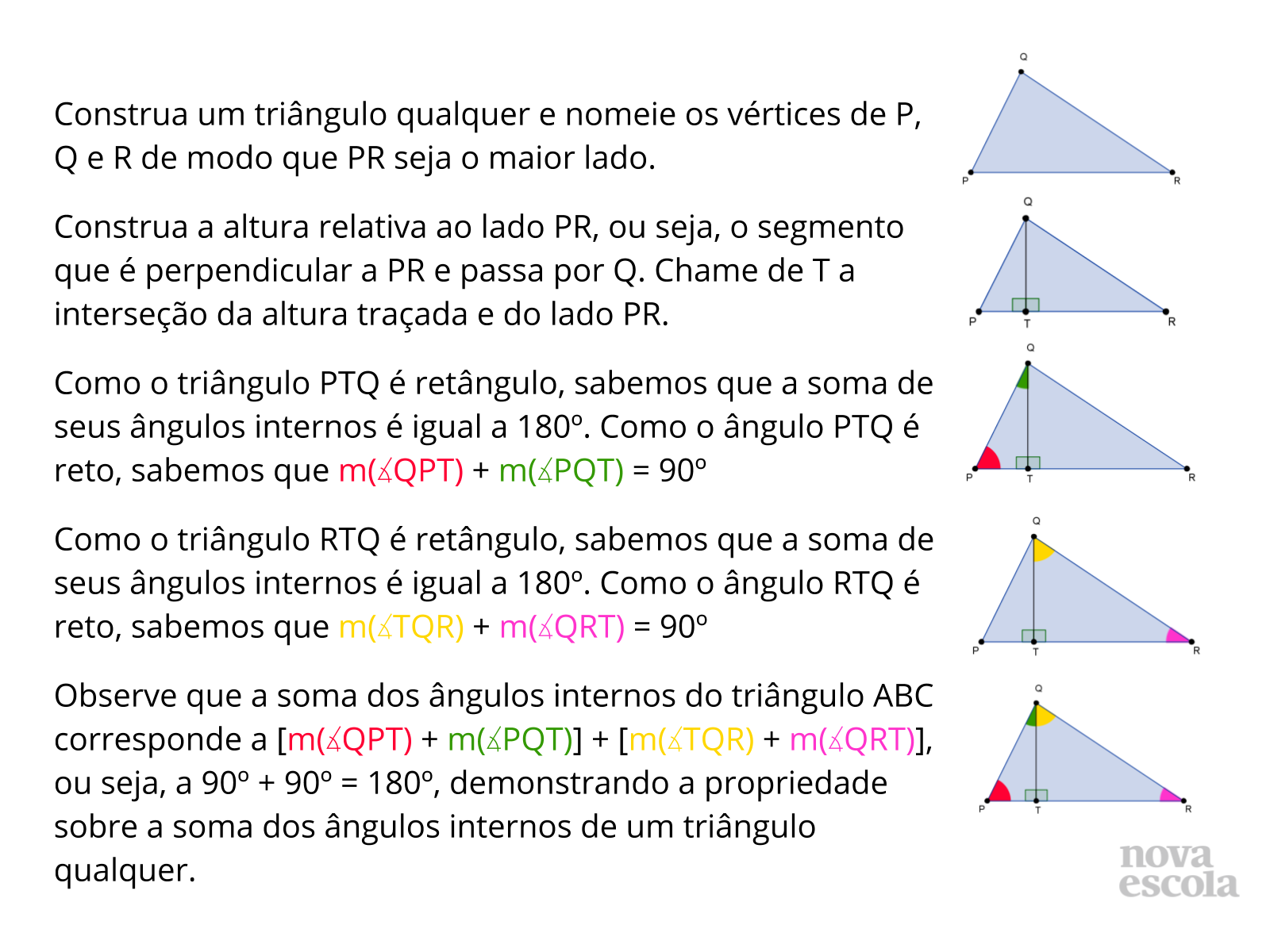
Orientações: Escolha um grupo para compartilhar a numeração escolhida para os parágrafos da demonstração da atividade 2. Abra para que os alunos digam se concordam ou não e que compartilhem outras possibilidades de numeração, se tiverem elaborado. Nesta discussão, é importante discutir a possibilidade de inverter a numeração dos parágrafos que destacam os ângulos internos dos triângulos PTQ e RTQ (veja a resolução da atividade para maiores detalhes). Discuta com a classe as estratégias que podem ser utilizadas para resolver problemas desse tipo (de decidir a ordem de parágrafos de uma demonstração). Depois, faça uma leitura coletiva da demonstração utilizando o slide 13. Esta leitura é interessante para aproximar os alunos da estrutura da demonstração e também para que eles compreendam a propriedade dos triângulos sobre a soma dos ângulos internos de maneira mais profunda.
Em seguida, peça para que os alunos leiam as demonstrações “oficiais” do grupo elaboradas na atividade 3 e que reproduzam na lousa as imagens que usaram para apoiar a demonstração. É importante que as diferentes respostas apareçam nesse momento e, por isso, a observação feita das resoluções dos alunos no momento anterior é muito importante para decidir quais grupos chamar para falar. Discuta com a classe se as demonstrações elaboradas estão corretas e completas, se são equivalentes e se estão escritas de um modo que facilita que o leitor as compreenda.
Por fim, se julgar necessário, exiba a demonstração do slide 15 ou escreva-a na lousa para concluir a discussão das soluções.
Propósito: propiciar que os alunos compreendam a estrutura das demonstrações, retomem propriedades de triângulos e quadriláteros e elaborem demonstrações próprias.
Discuta com a turma:
- Que estratégias podemos usar para identificar qual a ordem correta dos parágrafos da demonstração? As imagens podem ajudar? E os termos que aparecem nos parágrafos?
- A demonstração gerada na atividade 2 mostra por que a soma dos ângulos de um triângulo qualquer é sempre 180º? Elaborar esta demonstração é o mesmo que enunciar a propriedade?
- Que estratégias podemos usar para elaborar uma demonstração? Como podemos iniciá-la? E como deve ser a sua finalização?
- Como as imagens podem ajudar a deixar uma demonstração geométrica mais clara?
Painel de soluções

Tempo sugerido: 12 minutos (slides 12 a 15).
Orientações: Escolha um grupo para compartilhar a numeração escolhida para os parágrafos da demonstração da atividade 2. Abra para que os alunos digam se concordam ou não e que compartilhem outras possibilidades de numeração, se tiverem elaborado. Nesta discussão, é importante discutir a possibilidade de inverter a numeração dos parágrafos que destacam os ângulos internos dos triângulos PTQ e RTQ (veja a resolução da atividade para maiores detalhes). Discuta com a classe as estratégias que podem ser utilizadas para resolver problemas desse tipo (de decidir a ordem de parágrafos de uma demonstração). Depois, faça uma leitura coletiva da demonstração utilizando o slide 13. Esta leitura é interessante para aproximar os alunos da estrutura da demonstração e também para que eles compreendam a propriedade dos triângulos sobre a soma dos ângulos internos de maneira mais profunda.
Em seguida, peça para que os alunos leiam as demonstrações “oficiais” do grupo elaboradas na atividade 3 e que reproduzam na lousa as imagens que usaram para apoiar a demonstração. É importante que as diferentes respostas apareçam nesse momento e, por isso, a observação feita das resoluções dos alunos no momento anterior é muito importante para decidir quais grupos chamar para falar. Discuta com a classe se as demonstrações elaboradas estão corretas e completas, se são equivalentes e se estão escritas de um modo que facilita que o leitor as compreenda.
Por fim, se julgar necessário, exiba a demonstração do slide 15 ou escreva-a na lousa para concluir a discussão das soluções.
Propósito: propiciar que os alunos compreendam a estrutura das demonstrações, retomem propriedades de triângulos e quadriláteros e elaborem demonstrações próprias.
Discuta com a turma:
- Que estratégias podemos usar para identificar qual a ordem correta dos parágrafos da demonstração? As imagens podem ajudar? E os termos que aparecem nos parágrafos?
- A demonstração gerada na atividade 2 mostra por que a soma dos ângulos de um triângulo qualquer é sempre 180º? Elaborar esta demonstração é o mesmo que enunciar a propriedade?
- Que estratégias podemos usar para elaborar uma demonstração? Como podemos iniciá-la? E como deve ser a sua finalização?
- Como as imagens podem ajudar a deixar uma demonstração geométrica mais clara?
Painel de soluções
Tempo sugerido: 12 minutos (slides 12 a 15).
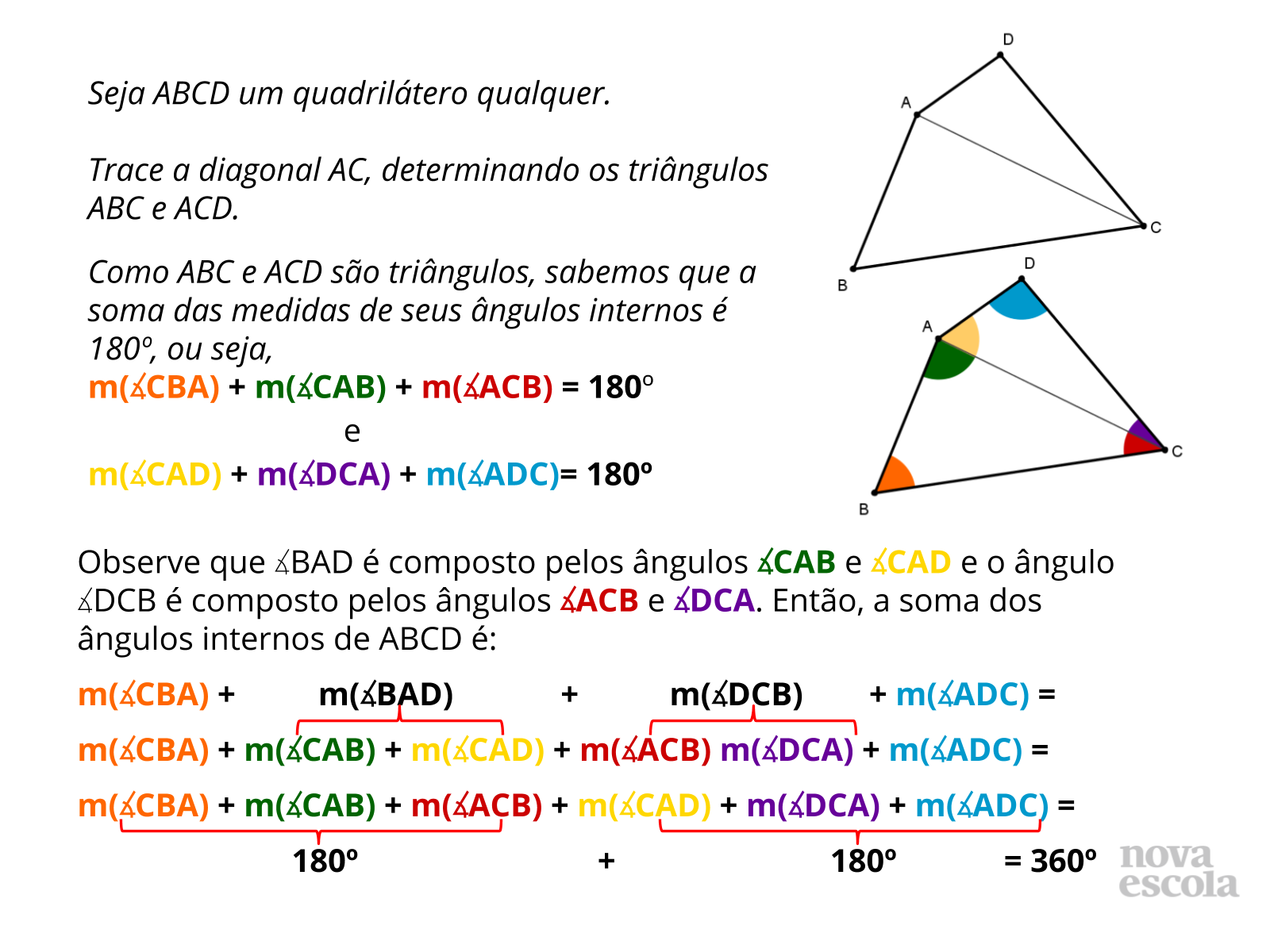
Orientações: Escolha um grupo para compartilhar a numeração escolhida para os parágrafos da demonstração da atividade 2. Abra para que os alunos digam se concordam ou não e que compartilhem outras possibilidades de numeração, se tiverem elaborado. Nesta discussão, é importante discutir a possibilidade de inverter a numeração dos parágrafos que destacam os ângulos internos dos triângulos PTQ e RTQ (veja a resolução da atividade para maiores detalhes). Discuta com a classe as estratégias que podem ser utilizadas para resolver problemas desse tipo (de decidir a ordem de parágrafos de uma demonstração). Depois, faça uma leitura coletiva da demonstração utilizando o slide 13. Esta leitura é interessante para aproximar os alunos da estrutura da demonstração e também para que eles compreendam a propriedade dos triângulos sobre a soma dos ângulos internos de maneira mais profunda.
Em seguida, peça para que os alunos leiam as demonstrações “oficiais” do grupo elaboradas na atividade 3 e que reproduzam na lousa as imagens que usaram para apoiar a demonstração. É importante que as diferentes respostas apareçam nesse momento e, por isso, a observação feita das resoluções dos alunos no momento anterior é muito importante para decidir quais grupos chamar para falar. Discuta com a classe se as demonstrações elaboradas estão corretas e completas, se são equivalentes e se estão escritas de um modo que facilita que o leitor as compreenda.
Por fim, se julgar necessário, exiba a demonstração do slide 15 ou escreva-a na lousa para concluir a discussão das soluções.
Propósito: propiciar que os alunos compreendam a estrutura das demonstrações, retomem propriedades de triângulos e quadriláteros e elaborem demonstrações próprias.
Discuta com a turma:
- Que estratégias podemos usar para identificar qual a ordem correta dos parágrafos da demonstração? As imagens podem ajudar? E os termos que aparecem nos parágrafos?
- A demonstração gerada na atividade 2 mostra por que a soma dos ângulos de um triângulo qualquer é sempre 180º? Elaborar esta demonstração é o mesmo que enunciar a propriedade?
- Que estratégias podemos usar para elaborar uma demonstração? Como podemos iniciá-la? E como deve ser a sua finalização?
- Como as imagens podem ajudar a deixar uma demonstração geométrica mais clara?
Encerramento

Tempo sugerido: 2 minutos.
Orientações: Projete e leia o texto desse slide (ou apenas leia, caso o recurso da projeção não esteja disponível) para sistematizar as aprendizagens da aula.
Propósito: Retomar as aprendizagens da aula, destacando as características das demonstrações e estratégias para elaborá-las.
Raio X
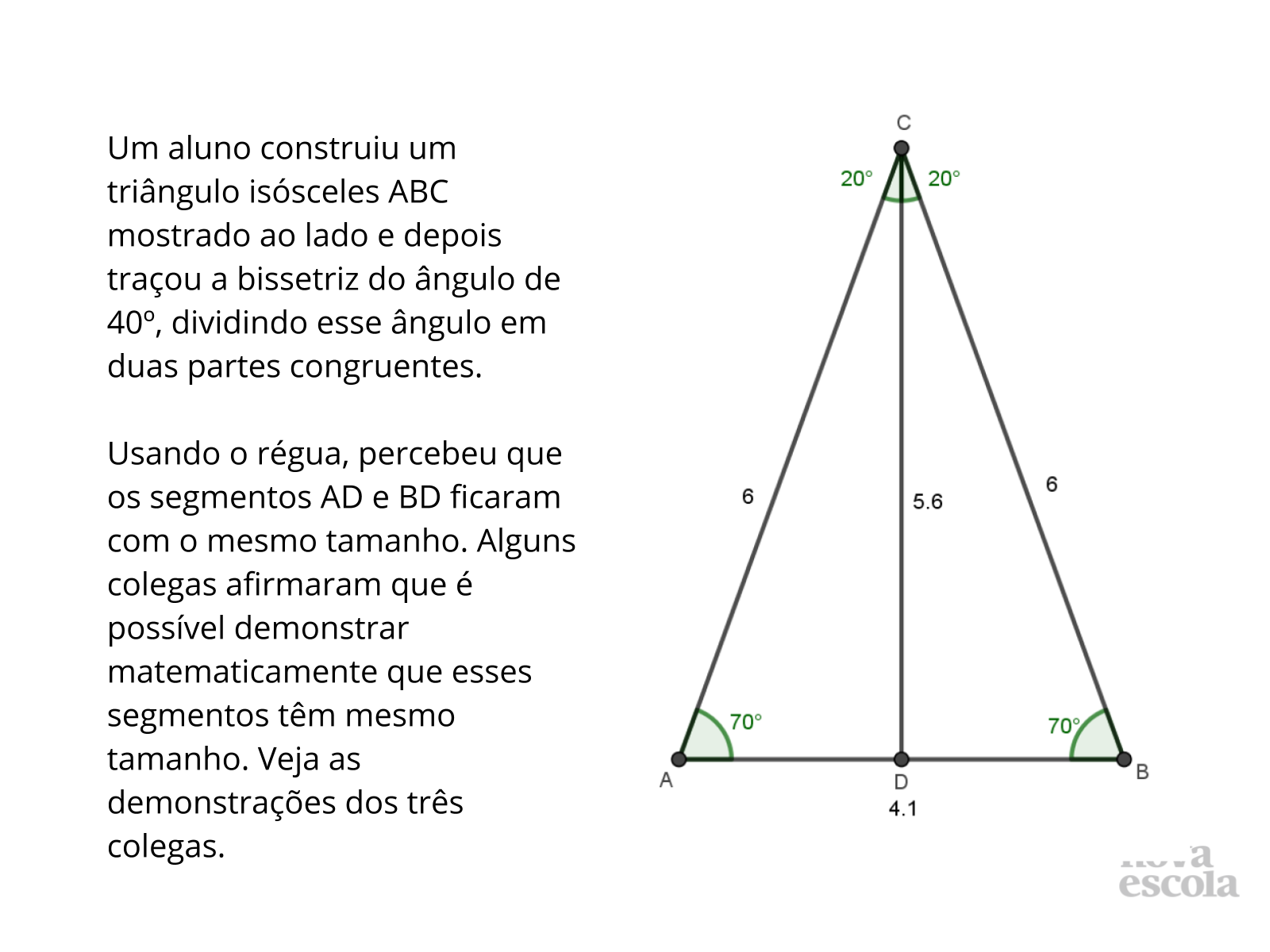
Tempo sugerido: 5 minutos (slides 17 e 18).
Orientações: Projete a atividade ou entregue cópias para os alunos e peça que, individualmente, leiam o enunciado e a realizem a atividade. Circule pela classe para verificar como os alunos estão realizando a tarefa e, caso algum aluno termine, solicite que ele verifique se a bissetriz também divide o lado oposto em dois segmentos congruentes em outros tipos de triângulos (sem ser isósceles). O raio X é um momento para você avaliar se todos os estudantes conseguiram avançar no conteúdo proposto, então procure identificar e anotar os comentários de cada um. No final, reserve um tempo para um debate coletivo.
Propósito: Verificar se os alunos aplicam os conhecimentos adquiridos numa situação semelhante e avaliar os conhecimentos de cada um a respeito das demonstrações matemáticas.
Materiais complementares para impressão:
Raio X
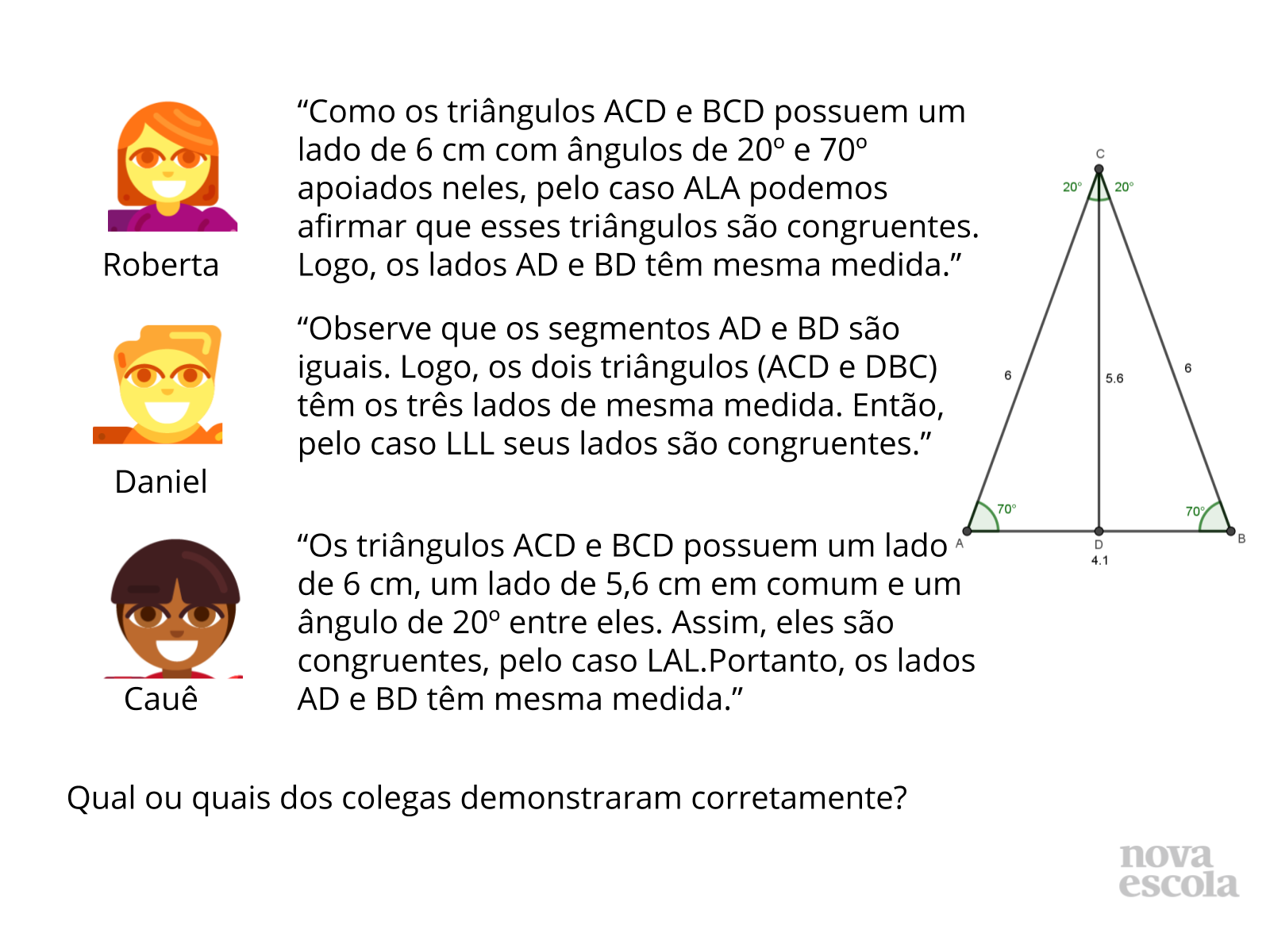
Tempo sugerido: 5 minutos (slides 17 e 18).
Orientações: Projete a atividade ou entregue cópias para os alunos e peça que, individualmente, leiam o enunciado e a realizem a atividade. Circule pela classe para verificar como os alunos estão realizando a tarefa e, caso algum aluno termine, solicite que ele verifique se a bissetriz também divide o lado oposto em dois segmentos congruentes em outros tipos de triângulos (sem ser isósceles). O raio X é um momento para você avaliar se todos os estudantes conseguiram avançar no conteúdo proposto, então procure identificar e anotar os comentários de cada um. No final, reserve um tempo para um debate coletivo.
Propósito: Verificar se os alunos aplicam os conhecimentos adquiridos numa situação semelhante e avaliar os conhecimentos de cada um a respeito das demonstrações matemáticas.
Materiais complementares para impressão:
Resolução da atividade complementar
Para os Alunos
Para o Professor
Sugestão de adaptação para ensino remoto
Código do plano
MAT8_15GEO10
Recursos
USAR APENAS FERRAMENTAS EM PORTUGUÊS E GRATUITAS
- Necessários: Papel, lápis, régua,WhatsApp
- Opcionais: Messenger Sala de aluno ( https://www.messenger.com/groupcall/LINK:4svjhs7dyZw8zoxm/), Meet, Hangout, Zoom, plataforma da Khan Academy ( https://pt.khanacademy.org/)
Portal OBMEP ( https://portaldaobmep.impa.br/index.php/modulo/lista?serie=3)
Geogebra https://play.google.com/store/apps/details?id=org.geogebra&hl=pt_BR
Para este plano, foque na etapa ATIVIDADE PRINCIPAL
Aquecimento
O aquecimento traz apenas uma reflexão. Você pode usá-la nas orientações.
Atividade principal
Use o passo a passo da demonstração da soma dos ângulos internos do triângulo para dar apoio a uma ‘aula invertida’ (Atividade 1). Peça que os alunos leiam e façam uma interpretação das informações, pontuando dúvidas. Para tal, você deve manter um canal de comunicação aberto. Solicite que os alunos gravem um vídeo explicando a demonstração da propriedade em discussão. Essa atividade pode ser desafiadora para os alunos. Talvez você precise apresentar algumas fontes de pesquisa para apoiar a atividade (há links abaixo que podem auxiliar) ou mesmo gravar um vídeo com dicas. Mas, a ideia é que os alunos estudem primeiro, pensem nos conceitos, construam propostas (vídeo), para posteriormente, nas discussões, haver o ‘fechamento’ da aula. Faça essa comunicação por WhatsApp ou em outra plataforma de comunicação como as indicadas nas Discussões. Sugerimos que use as Atividades 2 e 3 em outro momento, mas mantenha a proposta de discussão.
Na plataforma da Khan Academy há vários vídeos e demais recursos que tratam de soma de ângulos internos. Você pode selecionar os materiais pertinentes e indicar aos alunos que possuem acesso à internet.
https://pt.khanacademy.org/math/geometry/hs-geo-foundations/hs-geo-polygons/v/proof-sum-of-measures-of-angles-in-a-triangle-are-180
No Portal da OBMEP há exploração dos elementos básicos da geometria plana (partes 1, 2 e 3) que pode servir de apoio aos alunos que possuem internet.
https://portaldaobmep.impa.br/index.php/modulo/lista?serie
Discussão das soluções
Analise os vídeos apresentados pelos alunos para compor um áudio ou vídeo (WhatsApp) com feedback aos alunos. Selecione alguns vídeos para disponibilizar à turma inteira. Haverá a necessidade de novas discussões para as atividades 2 e 3 (Atividade principal). Não é interessante fazê-lo num único momento. Você pode fazer um ‘fechamento’ da aula através de um registro escrito. Se sua turma dispuser de ferramentas e internet, dê preferência por realizar as discussões em tempo real, por meio de uma das plataformas sugeridas abaixo. Se não tiver, use o WhatsApp que tem um alcance maior. Mas, não esqueça de manter um canal de comunicação para discussão também de sugerir a realização das demais atividades desse plano (atividades complementares e Raio X)
Se for possível discutir em tempo real com sua turma, use o Meet, Hangout ou Zoom e considere apenas os itens e os conceitos de maior relevância.
Você pode usar também o Messenger Sala de aluno https://www.messenger.com/groupcall/LINK:4svjhs7dyZw8zoxm/
Sistematização
xxxx
Encerramento
xxx
Raio X
Use o Raio X, as atividades complementares, as questões 2 e 3 da Atividade principal como forma de revisão para consolidação das aprendizagens. Não esqueça de retomar discussões também dessas atividades e focar nos pontos de aprendizagem mais críticos.
Convite às famílias
xxxx
Este plano de aula foi elaborado pelo Time de Autores NOVA ESCOLA
Autora: Renata Akemi Maekawa
Mentor: Fabricio Eduardo Ferreira
Especialista de área: Pricilla Cerqueira
Habilidade da BNCC
EF08MA12 - Demonstrar propriedades de quadriláteros por meio da identificação da congruência de triângulos.
EF08MA15 - Reconhecer e construir figuras obtidas por composições de transformações geométricas (translação, reflexão e rotação), com o uso de instrumentos de desenho ou de softwares de geometria dinâmica.
Objetivos específicos
-Retomar as propriedades sobre a soma dos ângulos internos de triângulos e quadriláteros.
-Retomar os critérios de congruência de triângulos.
-Compreender e elaborar demonstrações matemáticas.
Conceito-chave
Demonstrações matemáticas de propriedades geométricas
Recursos necessários
-Fichas impressas.
-Projetor (se possível)













